
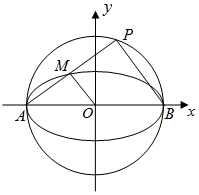
 已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.
已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.分析 (Ⅰ)由已知得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{b=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,求解方程组得a=2,则椭圆方程可求;
(Ⅱ)由已知可得PA⊥PB,结合|PB|=2|OM|且O为AB的中点,可得OM为的△ABP中位线,且OM⊥AP.设出点M的坐标,由点在椭圆上及OM⊥AM得关于s,t的方程组,求得s,t的值,再由中点坐标公式求得点P的坐标.
解答 解:(Ⅰ)由已知得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{b=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1.
∴椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)∵点P在曲线C1上,∴PA⊥PB,
又∵|PB|=2|OM|,且O为AB的中点,
∴OM为的△ABP中位线,且OM⊥AP.
否则|PB|<2|OM|,与|PB|=2|OM|矛盾.
设点M的坐标为(s,t),
∵点M在曲线C上,∴s2+4t2-4=0,①
∵OM⊥AM,∴(s+1)2+t2=1,②
由②得:t2=1-(s+1)2,代入①整理得:3s2+8s+4=0.
解得:$s=-\frac{2}{3}$或s=-2(舍),∴$t=±\frac{{2\sqrt{2}}}{3}$,
设点P的坐标为(x0,y0)
则 $\frac{{-2+{x_0}}}{2}=-\frac{2}{3},\;\frac{y_0}{2}=±\frac{{2\sqrt{2}}}{3}$,
∴${x_0}=\frac{2}{3},{y_0}=±\frac{{4\sqrt{2}}}{3}$.
∴点P的坐标为$(-\frac{2}{3},±\frac{{4\sqrt{2}}}{3})$.
点评 本题考查椭圆的简单性质,考查直线与圆、椭圆位置关系的应用,考查计算能力,是中档题.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:解答题
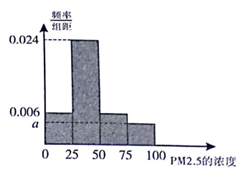 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-2,1) | C. | (1,+∞) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com