
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①若am2<bm2,可知,m2>0,则a<b
②由题意,根据一次项系数的符号判断相关性,由y与z正相关,设y=kz,k>0,得到x与z的相关性.
③若m⊥n,m⊥α,n∥β,则α、β的位置关系不定
④当m=0时,直线(m+3)x+my-2=0与直线mx-6y+5=0也互相垂直.
解答 解:对于①,若am2<bm2,可知,m2>0,则a<b,故正确;
对于②,因为变量x和y满足关系y=-0.1x+1,一次项系数为-0.1<0,所以x与y负相关;
变量y与z正相关,设,y=kz,(k>0),所以kz=-0.1x+1,得到z=-$\frac{0.1}{k}+\frac{1}{k}$,一次项系数小于0,所以z与x负相关,故正确;
对于③,若m⊥n,m⊥α,n∥β,则α、β的位置关系不定,故错
对于④,当m=0时,直线(m+3)x+my-2=0与直线mx-6y+5=0也互相垂直,故错;
故选:B.
点评 本题考查了命题真假判定,涉及到了大量的基础知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | k=±2 | B. | k=$\frac{8}{{e}^{2}}$ | C. | k=2 | D. | k=$\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
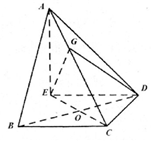 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | (12,22] | (22,32] | (32,42] | (42,52] | (52,62] | (62,72] |
| 频数 | m | 3 | 7 | 5 | 4 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
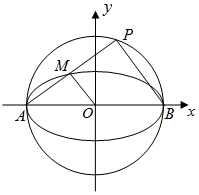 已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.
已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com