
分析 (Ⅰ)先求导,再由导函数为0,解得即可;
(Ⅱ)根据(Ⅰ)分类讨论,分别利用导数和函数的最值的关系以及充分不必要条件的定义即可证明.
解答 解:(Ⅰ)由f(x)=(x2+ax-a)•e1-x,
得f′(x)=(2x+a)e1-x-(x2+ax-a)•e1-x=-[x2+(a-2)x-2a]•e1-x=-(x+a)(x-2)•e1-x,
令f′(x)=0,得x=2,或x=-a.
所以当a=-2时,函数f′(x)有且只有一个零点:x=2;
当a≠-2时,函数f′(x)有两个相异的零点:x=2,x=-a.
(Ⅱ)证明:①当a=-2时,f′(x)≤0恒成立,此时函数f(x)在(-∞,+∞)上单调递减,
所以,函数f(x)无极值.
②当a>-2时,f′(x),f(x)的变化情况如下表:
| x | (-∞,-a) | -a | (-a,2) | 2 | (2,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
| x | (-∞,2) | 2 | (2,5) | 5 | (5,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
点评 本题考查了导数和函数的极值和最值的关系,考查了学生的运算能力和转化能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
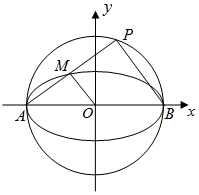 已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.
已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
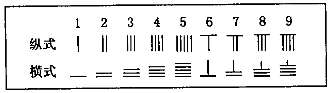
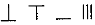 ,则5288用算筹式可表示为
,则5288用算筹式可表示为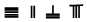 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
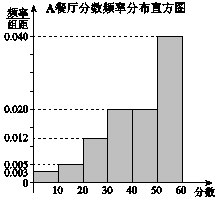 某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:| B餐厅分数频数分布表 | |
| 分数区间 | 频数 |
| [0,10) | 2 |
| [10,20) | 3 |
| [20,30) | 5 |
| [30,40) | 15 |
| [40,50) | 40 |
| [50,60] | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com