
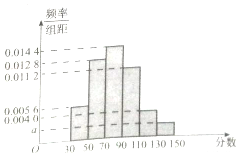
 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)分析 (1)由题意和频率分布直方图列出方程,求出a,由此能求出这500名学生中进入决赛的人数,及进入决赛学生的平均分.
(2)成绩在130分以上的学生数X是一个随机变量,其可能取值为0,1,2,3,X~B(3,$\frac{1}{3}$),由此能求出X的分布列、数学期望及方差.
解答 解:(1)由题意和频率分布直方图,得:
$\frac{500}{500×20}=0.014$4+0.0128+0.0112+0.0056+0.0040+a,
解得a=0.0020,
∴这500名学生中进入决赛的人数为:(0.0040+0.0020)×500×20=60,
进入决赛学生的平均分为:
40×0.0056×20+60×0.0128×20+80×0.0144×20+100×0.0112×20+120×0.0040×20+140×0.0020×20=80.48≈80.5,
∴这500名学生中有60人进入决赛,进入决赛学生的平均分为80.5分.
(2)∵进入决赛的60名学生中,成绩在130分以上的学生有20人,
用频率估计概率,则学生成绩在[110,130)之间的概率为$\frac{2}{3}$,
在[130,150]之间的概率为$\frac{1}{3}$,
成绩在130分以上的学生数X是一个随机变量,其可能取值为0,1,2,3,
P(X=0)=${C}_{3}^{0}×(\frac{2}{3})^{3}×(\frac{1}{3})^{0}=\frac{8}{27}$,
P(X=1)=${C}_{3}^{1}×(\frac{2}{3})^{2}×(\frac{1}{3})=\frac{12}{27}$,
P(X=2)=${C}_{3}^{2}×(\frac{2}{3})×(\frac{1}{3})^{2}$=$\frac{6}{27}$,
P(X=3)=${C}_{3}^{3}(\frac{2}{3})^{0}(\frac{1}{3})^{3}=\frac{1}{27}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{8}{27}$ | $\frac{12}{27}$ | $\frac{6}{27}$ | $\frac{1}{27}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望、方差的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,是中档题.


科目:高中数学 来源: 题型:选择题
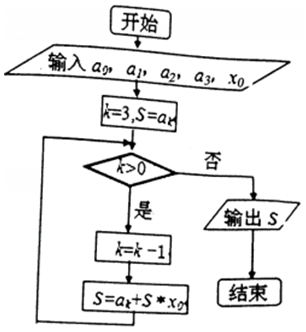
| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1300 | C. | 2600 | D. | 2602 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
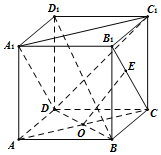 在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则
在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
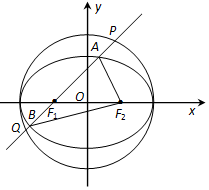 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com