练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．如图是秦九韶算法的一个程序框图，则输出的S为（　　）
    A．a1+x0（a3+x0（a0+a2x0））的值B．a3+x0（a2+x0（a1+a0x0））的值
    C．a0+x0（a1+x0（a2+a3x0））的值D．a2+x0（a0+x0（a3+a1x0））的值

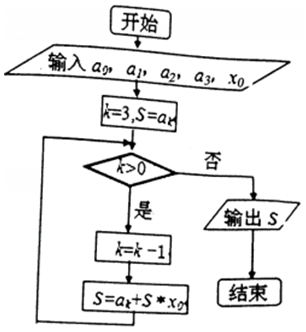
    分析 模拟程序的运行，依次写出每次循环得到的k，S的值，当k=0时，不满足条件k＞0，退出循环，输出S的值为a0+x0（a1+x0（a2+a3x0））．

    解答 解：模拟程序的运行，可得
    k=3，S=a3，
    满足条件k＞0，执行循环体，k=2，S=a2+a3x0，
    满足条件k＞0，执行循环体，k=1，S=a1+x0（a2+a3x0），
    满足条件k＞0，执行循环体，k=0，S=a0+x0（a1+x0（a2+a3x0）），
    不满足条件k＞0，退出循环，输出S的值为a0+x0（a1+x0（a2+a3x0））．
    故选：C．

    点评 本题主要考查了循环结构的程序框图的应用，依次正确写出每次循环得到的S，k的值是解题的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．已知△ABC是正三角形，O是△ABC的中心，D和E分别是边AB和AC的中点，若$\overrightarrow{OA}=x\overrightarrow{OD}+y\overrightarrow{OE}$，则x+y=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．如图，“赵爽弦图”是由四个全等的直角三角形（阴影部分）围成一个大正方形，中间空出一个小正方形组成的图形，若在大正方形内随机取一点，该点落在小正方形的概率为$\frac{1}{5}$，则图中直角三角形中较大锐角的正弦值为（　　）
    A．$\frac{\sqrt{5}}{5}$B．$\frac{2\sqrt{5}}{5}$C．$\frac{1}{5}$D．$\frac{\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．我们知道：“平面中到定点等于定长的点轨迹是圆”拓展至空间：“空间中到定点的距离等于定长的点的轨迹是球”，类似可得：已知A（-1，0，0），B（1，0，0），则点集{P（x，y，z）||PA|-|PB|=1}在空间中的轨迹描述正确的是（　　）
    A．以A，B为焦点的双曲线绕轴旋转而成的旋转曲面
    B．以A，B为焦点的椭球体
    C．以A，B为焦点的双曲线单支绕轴旋转而成的旋转曲面
    D．以上都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

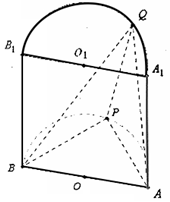    2．如图半圆柱OO1的底面半径和高都是1，面ABB1A1是它的轴截面（过上下底面圆心连线OO1的平面），Q，P分别是上下底面半圆周上一点．
    （1）证明：三棱锥Q-ABP体积VQ-ABP≤$\frac{1}{3}$，并指出P和Q满足什么条件时有AP⊥BQ
    （2）求二面角P-AB-Q平面角的取值范围，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知曲线C1的参数方程为$\left\{\begin{array}{l}x=5+5cost\\ y=4+5sint\end{array}\right.$（t为参数）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2cosθ．
    （Ⅰ）把C1的参数方程化为极坐标方程；
    （Ⅱ）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设函数f（x）=ax+bx-cx，其中c＞a＞0，c＞b＞0．若a、b、c是△ABC的三条边长，则下列结论中正确的个数是（　　）
    ①对于一切x∈（-∞，1）都有f（x）＞0；
    ②存在x＞0使ax，bx，cx不能构成一个三角形的三边长；
    ③若△ABC为钝角三角形，则存在x∈（1，2），使f（x）=0．
    A．3个B．2个C．1个D．0个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．袋中装有除颜色外形状大小完全相同的6个小球，其中有4个编号为1，2，3，4的红球，2个编号为A、B的黑球，现从中任取2个小球．
    （Ⅰ）求所取取2个小球都是红球的概率；
    （Ⅱ）求所取的2个小球颜色不相同的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

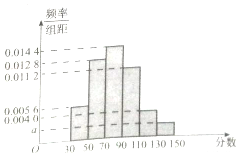    17．某市高二年级学生进行数学竞赛，竞赛分为初赛和决赛，规定成绩在110分及110分以上的学生进入决赛，110分以下的学生则被淘汰，现随机抽取500名学生的初赛成绩按[30，50），[50，70），[70，90），[90，110），[110，130），[130，150]做成频率副本直方图，如图所示：（假设成绩在频率分布直方图中各段是均匀分布的）
    （1）求这500名学生中进入决赛的人数，及进入决赛学生的平均分（结果保留一位小数）；
    （2）用频率估计概率，在全市进入决赛的学生中选取三人，其中成绩在[130，150]的学生数为X，试写出X的分布列，并求出X的数学期望及方差．

    查看答案和解析>>

    同步练习册答案