
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 ①利用指数函数的性质以a.b.c构成三角形的条件进行证明;
②可以举反例进行判断;
③利用函数零点的存在性定理进行判断.
解答 解:对于①,a,b,c是△ABC的三条边长,∴a+b>c,
∵c>a>0,c>b>0,∴0<$\frac{a}{c}$<1,0<$\frac{b}{c}$<1,
当x∈(-∞,1)时,f(x)=ax+bx-cx=cx[${(\frac{a}{c})}^{x}$+${(\frac{b}{c})}^{x}$-1]
>cx•($\frac{a}{c}$+$\frac{b}{c}$-1)=cx•$\frac{a+b-c}{c}$>0,∴①正确;
对于②,令a=2,b=3,c=4,则a,b,c可以构成三角形,
但a2=4,b2=9,c2=16却不能构成三角形,∴②正确;
对于③,c>a>0,c>b>0,若△ABC为钝角三角形,则a2+b2-c2<0,
∵f(1)=a+b-c>0,f(2)=a2+b2-c2<0,
∴由根的存在性定理可知在区间(1,2)上存在零点,
即?x∈(1,2),使f(x)=0,∴③正确;
综上,正确命题的个数为3个.
故选:A.
点评 本题考查了函数零点的存在性定理,指数函数的性质,以及余弦定理的应用问题,是综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
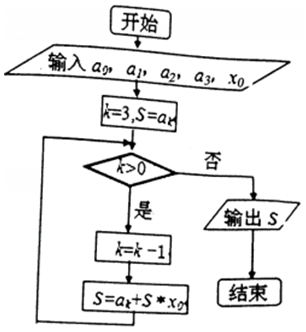
| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
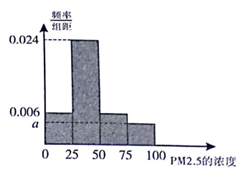 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-2,-1,0,1} | C. | {-2,-1,0} | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
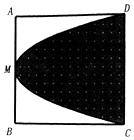 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1300 | C. | 2600 | D. | 2602 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com