
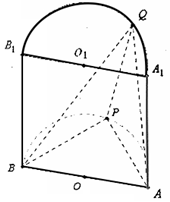
 如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.
如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.分析 (1)由条件及圆柱性质知平面A1B1Q到ABP的距离且为定值1,由半圆性质∠APB=90°,所以AP2+BP2=4
所以由均值不等式s△ABP=$\frac{1}{2}AP•BP≤\frac{A{P}^{2}+B{P}^{2}}{4}=1$.得VQ-ABP=$\frac{1}{3}{s}_{△ABP}×h$≤$\frac{1}{3}$
由AP⊥PB可知,要有AP⊥BQ,只需要PQ⊥PA即可
(2)以O为原点、OA为x轴、OO1为z轴建坐标系作QN垂直于平面ABP于N,记∠AON=θ,θ∈[0,π],A(1,O,O),B(-1,0,0),Q(cosθ,sinθ,0)
平面PAB法向量可取$\overrightarrow{n}=(0,0,1)$
设平面ABQ的法向量$\overrightarrow{m}=(x,y,z)$,可取$\overrightarrow{m}=(0,-1,sinθ)$
θ∈(0,$\frac{π}{2}$]时,|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=$\frac{sinθ}{\sqrt{1+si{n}^{2}θ}}=\left\{\begin{array}{l}{0,(θ=0)}\\{\frac{1}{\sqrt{sinθ+\frac{1}{sinθ}}}}\end{array}\right.$即可求二面角P-AB-Q平面角的取值范围
解答 解:(1)证明:VQ-ABP=$\frac{1}{3}{s}_{△ABP}×h$,其中h是Q到平面ABP的距离,(由条件及圆柱性质)即平面A1B1Q到ABP的距离且为定值1
由半圆性质∠APB=90°,所以AP2+BP2=4
所以由均值不等式s△ABP=$\frac{1}{2}AP•BP≤\frac{A{P}^{2}+B{P}^{2}}{4}=1$.
∴VQ-ABP=$\frac{1}{3}{s}_{△ABP}×h$≤$\frac{1}{3}$
因为AP⊥PB,要有AP⊥BQ,只需要PQ⊥PA即可!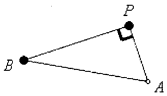
(2)
如图以O为原点、OA为x轴、OO1为z轴建坐标系作QN垂直于平面ABP于N,
记∠AON=θ,θ∈[0,π]
A(1,O,O),B(-1,0,0),Q(cosθ,sinθ,0)
平面PAB法向量可取$\overrightarrow{n}=(0,0,1)$
设平面ABQ的法向量$\overrightarrow{m}=(x,y,z)$,$\overrightarrow{AQ}=(cosθ-1,sinθ,1)$,$\overrightarrow{BA}=(2,0,0)$
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BA}=x(cosθ-1)+ysinθ+z=0}\\{\overrightarrow{m}•\overrightarrow{BQ}=2x=0}\end{array}\right.$,可取$\overrightarrow{m}=(0,-1,sinθ)$
∴θ∈(0,$\frac{π}{2}$]时,|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=$\frac{sinθ}{\sqrt{1+si{n}^{2}θ}}=\left\{\begin{array}{l}{0,(θ=0)}\\{\frac{1}{\sqrt{sinθ+\frac{1}{sinθ}}}}\end{array}\right.$
θ∈(0,$\frac{π}{2}$]时,sinθ+$\frac{1}{sinθ}$≥2.(当sinθ=1时取等号)
|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|∈[0,$\frac{\sqrt{2}}{2}$],
所以二面角P-AB-Q平面角的取值范围是:[$\frac{π}{4}$,$\frac{π}{2}$]
点评 本题考查了圆柱的性质,空间线面、线线位置关系,向量法求二面角的取值范围,属于难题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | 1>($\frac{1}{2}$)b>($\frac{1}{2}$)a | C. | $\frac{b}{a}$+$\frac{a}{b}$<2 | D. | aeb>bea |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
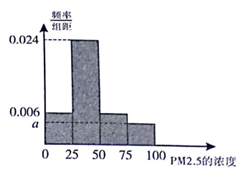 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
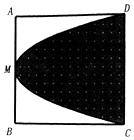 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com