若$\frac{1}{a}$＜$\frac{1}{b}$＜0.则下列结论正确的是( )A．a2＞b2B．1＞b＞aC．$\frac{b}{a}$+$\frac{a}{b}$＜2D．aeb＞bea 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

17．若$\frac{1}{a}$＜$\frac{1}{b}$＜0，则下列结论正确的是（　　）

A．

a²＞b²

B．

1＞（$\frac{1}{2}$）^b＞（$\frac{1}{2}$）^a

C．

$\frac{b}{a}$+$\frac{a}{b}$＜2

D．

ae^b＞be^a

分析由题意，b＜a＜0，分别判断选项，即可得出结论．

解答解：由题意，b＜a＜0，则a²＜b²，（$\frac{1}{2}$）^b＞（$\frac{1}{2}$）^a＞1，$\frac{b}{a}$+$\frac{a}{b}$＞2，
∵b＜a＜0，∴e^a＞e^b＞0，-b＞-a＞0
∴-be^a＞-ae^b，∴ae^b＞be^a，
故选D．

点评本题考查不等式的性质，考查学生的计算能力，比较基础．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

7．设向量$\overrightarrow{a}$=（2，m），$\overrightarrow{b}$=（3，-1），若$\overrightarrow{a}$⊥（$\overrightarrow{a}$-2$\overrightarrow{b}$），则实数m=（　　）

A．

2或-4

B．

C．

-$\frac{1}{4}$或$\frac{1}{2}$

D．

-4

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．已知函数f（x）=2sinx•sin（x+$\frac{π}{3}$）．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）锐角△ABC的角A，B，C所对边分别是a，b，c，角A的平分线交BC于D，直线x=A是函数f（x）图象的一条对称轴，AD=$\sqrt{2}$BD=2，求边a．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．已知f（x）=x²•e^x，若函数g（x）=f²（x）-kf（x）+1恰有三个零点，则下列结论正确的是（　　）

A．

k=±2

B．

k=$\frac{8}{{e}^{2}}$

C．

k=2

D．

k=$\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．《九章算术》卷第六《均输》中，有问题“今有竹九节，下三节容量四升，上四节容量三升．问中间二节欲均容，各多少？”其中“欲均容”的意思是：使容量变化均匀，即由下往上均匀变细．在这个问题中的中间两节容量和是（　　）

A．

$1\frac{61}{66}$升

B．

2升

C．

$2\frac{3}{22}$升

D．

3升

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．

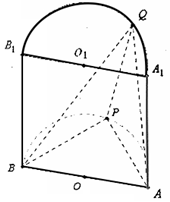如图半圆柱OO₁的底面半径和高都是1，面ABB₁A₁是它的轴截面（过上下底面圆心连线OO₁的平面），Q，P分别是上下底面半圆周上一点．
（1）证明：三棱锥Q-ABP体积V_Q-ABP≤$\frac{1}{3}$，并指出P和Q满足什么条件时有AP⊥BQ
（2）求二面角P-AB-Q平面角的取值范围，并说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

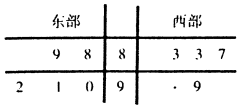某省电视台为了解该省卫视一档成语类节目的收视情况，抽查东西两部各5个城市，得到观看该节目的人数（单位：千人）如下茎叶图所示：
其中一个数字被污损．
（1）求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率．
（2）随着节目的播出，极大激发了观众对成语知识的学习积累的热情，从中获益匪浅．现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间y（单位：小时）与年龄x（单位：岁），并制作了对照表（如表所示）

年龄x（岁）	20	30	40	50
周均学习成语知识时间y（小时）	2.5	3	4	4.5

由表中数据，试求线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并预测年龄为55岁观众周均学习成语知识时间．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2|$\overrightarrow{a}$|，且（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{a}$，则$\overrightarrow{a}$，$\overrightarrow{b}$的夹角等于（　　）

A．

$\frac{2π}{3}$

B．

$\frac{5π}{6}$

C．

$\frac{π}{3}$

D．

$\frac{π}{6}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．已知△ABC中，角A，B，C所对的边依次为a，b，c，其中b=2．
（Ⅰ）若asin2B=$\sqrt{3}$bsinA，求B；
（Ⅱ）若a，b，c成等比数列，求△ABC面积的最大值．

查看答案和解析>>

同步练习册答案