
| A. | m>n | B. | m<n | C. | m=n | D. | 大小不确定 |
分析 $\frac{m-n}{b}=\frac{a+blnb-b-blna}{b}$=$\frac{a}{b}-1+ln\frac{b}{a}$,令t=$\frac{a}{b}>1$,则f(t)=t-1-lnt,${f}^{'}(t)=1-\frac{1}{t}=\frac{t-1}{t}$>0,从而f(t)是增函数,由此能求出m>n.
解答 解:∵m=a+blnb,n=b+blna,a>b>0,
∴$\frac{m-n}{b}=\frac{a+blnb-b-blna}{b}$
=$\frac{a}{b}-1+ln\frac{b}{a}$,
∵a>b>0,∴令t=$\frac{a}{b}>1$,
∴f(t)=t-1+ln$\frac{1}{t}$=t-1-lnt,
${f}^{'}(t)=1-\frac{1}{t}=\frac{t-1}{t}$>0,∴f(t)是增函数,
∵f(1)=1-1-ln1=0,∴f(t)>0,
∴m>n.
故选:A.
点评 本题考查两个数的大小的比较,是中档题,解题时要认真审题,注意作差法和对数性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或-4 | B. | 2 | C. | -$\frac{1}{4}$或$\frac{1}{2}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩∁RN=φ | B. | M∪N=R | C. | ∁RM∪N=R | D. | M∩N=M |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
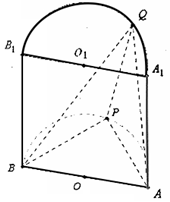 如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.
如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com