
分析 (1)求出C1,C2的普通方程,即可求C1,C2的极坐标方程;
(2)利用极径的意义,求线段AB的长度.
解答 解:(1)设点P(x,y),M(2cosα,2+2sinα),
则由$\overrightarrow{OP}=2\overrightarrow{OM}$得:x=4cosα,y=4+4sinα,消参得:x2+(y-4)2=16.
转化为极坐标方程得:ρ=8sinθ,所以C2的极坐标方程ρ=8sinθ,
同理可得C1的极坐标方程ρ=4sinθ.
(2)在极坐标系,可得$OA=ρ=4sin\frac{π}{3}=2\sqrt{3}$,$OB=ρ=8sin\frac{π}{3}=4\sqrt{3}$,
所以$|AB|=OB-OA=2\sqrt{3}$.
点评 本题考查三种方程的转化,考查极径的意义,属于中档题.


科目:高中数学 来源: 题型:解答题
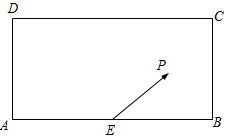 某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.
某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,$\frac{π}{2}$),x>sinx | |
| B. | 在△ABC中,若A>B,则sinA>sinB | |
| C. | 函数f(x)=tanx图象的一个对称中心是($\frac{π}{2}$,0) | |
| D. | ?x0∈R,sinx0cosx0=$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com