
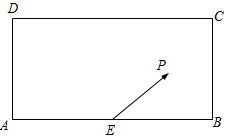
 某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.
某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.分析 (1)利用正弦定理,即可求解;
(2)以AB所在直线为x轴,AB中垂线为y轴,建平面直角坐标系,求出Q的轨迹方程,即可得出结论.
解答 解:(1)△AEQ中,AQ=2EQ,∠AEQ=120°…(2分)
由正弦定理,得:$\frac{EQ}{sin∠QAE}=\frac{AQ}{sin∠AEQ}$
所以$sin∠QAE=\frac{{\sqrt{3}}}{4}$…(4分)
所以$∠QAE=arcsin\frac{{\sqrt{3}}}{4}≈25.7°$
所以应在矩形区域ABCD内,按照与$\overrightarrow{AB}$夹角为25.7°的向量$\overrightarrow{AQ}$方向释放机器人乙,才能挑战成功…(6分)
(2)以AB所在直线为x轴,AB中垂线为y轴,建平面直角坐标系,
设Q(x,y)(y≥0)…(8分)
由题意,知AQ=2EQ,所以$\sqrt{{{(x+9)}^2}+{y^2}}=2\sqrt{{x^2}+{y^2}}$
所以(x-3)2+y2=36(y≥0)…(11分)
即点Q的轨迹是以(3,0)为圆心,6为半径的上半圆在矩形区域ABCD内的部分
所以当AD≥6米时,能确保无论θ的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域ABCD内成功拦截机器人甲…(14分)
点评 本题考查轨迹方程,考查正弦定理的运用,考查学生的计算能力,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
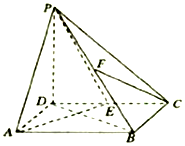 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别是CD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别是CD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ | D. | $\sqrt{3}$或$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com