练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．在△ABC中，若AC=5，BC=6，sinA=$\frac{3}{5}$，则角B的大小为30°．

    分析 运用正弦定理可得$\frac{AC}{sinB}$=$\frac{BC}{sinA}$，代入数据，可得sinB，再由B＜A，即可得到所求角B．

    解答 解：在△ABC中，若AC=5，BC=6，sinA=$\frac{3}{5}$，
    由正弦定理可得，$\frac{AC}{sinB}$=$\frac{BC}{sinA}$，
    即为sinB=$\frac{ACsinA}{BC}$=$\frac{5×\frac{3}{5}}{6}$=$\frac{1}{2}$，
    由AC＜BC，可得B＜A，
    则B=30°（150°舍去），
    故答案为：30°．

    点评 本题考查解三角形的正弦定理的运用，同时考查三角形的边角关系，考查运算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．数列{an}中，a1=$\frac{1}{2}$，an+1=$\frac{{{a}_{n}}^{2}}{{{a}_{n}}^{2}-{a}_{n}+1}$（n∈N*）
    （Ⅰ）求证：an+1＜an；
    （Ⅱ）记数列{an}的前n项和为Sn，求证：Sn＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知函数f（x）=$\left\{\begin{array}{l}{x+2，x＜0}\\{3x-1，x≥0}\end{array}\right.$，则f[f（-1）]=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，则下列关系可以成立的而是（　　）
    A．（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{a}$B．（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥（$\overrightarrow{a}$+$\overrightarrow{b}$）C．（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{b}$D．（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{a}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某供货商计划将某种大型节日商品分别配送到甲、乙两地销售．据以往数据统计，甲、乙两地该商品需求量的频率分布如下：
    甲地需求量频率分布表示：
    需求量456
    频率0.50.30.2
    乙地需求量频率分布表：
    需求量345
    频率0.60.30.1
    以两地需求量的频率估计需求量的概率
    （Ⅰ）若此供货商计划将10件该商品全部配送至甲、乙两地，为保证两地不缺货（配送量≥需求量）的概率均大于0.7，问该商品的配送方案有哪几种？
    （Ⅱ）已知甲、乙两地该商品的销售相互独立，该商品售出，供货商获利2万元/件；未售出的，供货商亏损1万元/件．在（Ⅰ）的前提下，若仅考虑此供货商所获净利润，试确定最佳配送方案．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

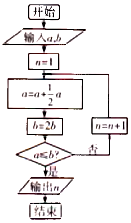    13．《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物，包括面积、体积、比例、开方、高次方程等问题，《算学启蒙》中有关于“松竹并生”的问题：“松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等”，如图是源于其思想的一个程序框图，若输入a，b分别为8，2，则输出的n等于（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

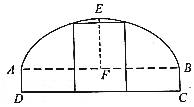    20．如图所示，一辆装载集装箱的载重卡车高为3米，宽为2.2米，欲通过断面上部为抛物线形，下部为矩形ABCD的隧道．已知拱口宽AB等于拱高EF的4倍，AD=1米．若设拱口宽度为t米，则能使载重卡车通过隧道时t的最小整数值等于9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知实数x，y满足$\left\{\begin{array}{l}{3x+y-7≥0}\\{x+3y-13≤0}\\{x-y-1≤0}\end{array}\right.$，则z=|2x-3y+4|的最大值为（　　）
    A．3B．5C．6D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

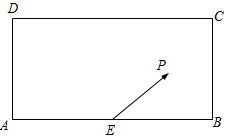    18．某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛，在E处按$\overrightarrow{EP}$方向释放机器人甲，同时在A处按某方向释放机器人乙，设机器人乙在Q处成功拦截机器人甲．若点Q在矩形区域ABCD内（包含边界），则挑战成功，否则挑战失败．
    已知AB=18米，E为AB中点，机器人乙的速度是机器人甲的速度的2倍，比赛中两机器人均按匀速直线运动方式行进，记$\overrightarrow{EP}$与$\overrightarrow{EB}$的夹角为θ．
    （1）若θ=60°，AD足够长，则如何设置机器人乙的释放角度才能挑战成功？（结果精确到0.1°）
    （2）如何设计矩形区域ABCD的宽AD的长度，才能确保无论θ的值为多少，总可以通过设置机器人乙的释放角度使机器人乙在矩形区域ABCD内成功拦截机器人甲？

    查看答案和解析>>

    同步练习册答案