
分析 (Ⅰ)由已知利用三角形内角和定理,两角和的正切函数公式可求tanB的值,结合范围0<B<π,可求B的值.
(Ⅱ)由(Ⅰ)知$α+β=\frac{3π}{4}$,利用三角函数恒等变换的应用化简可得$\sqrt{2}$sinα-sinβ=sin(α-$\frac{π}{4}$),结合范围$0<α<\frac{3π}{4}$,利用正弦函数的图象和性质可求其取值范围.
解答 解:(Ⅰ)∵A+B+C=π,
∴B=π-(A+C),
又$tanA=\frac{1}{3}$,$tanC=\frac{1}{2}$,
则$tanB=tan[{π-(A+C)}]=-tan(A+C)=-\frac{tanA+tanC}{1-tanAtanC}=-1$,
∵B为△ABC的内角,
∴$B=\frac{3π}{4}$.
(Ⅱ)∵α+β=B(α>0,β>0),
∴$α+β=\frac{3π}{4}$.
∵$\sqrt{2}sinα-sinβ=\sqrt{2}sinα-sin(\frac{3π}{4}-α)=\sqrt{2}sinα-(\frac{{\sqrt{2}}}{2}cosα+\frac{{\sqrt{2}}}{2}sinα)$=$sin(α-\frac{π}{4})$,
又α+β=B(α>0,β>0),
则$α∈(0,\frac{3π}{4})$,$α-\frac{π}{4}∈(-\frac{π}{4},\frac{π}{2})$,
∴$sin(α-\frac{π}{4})∈(-\frac{{\sqrt{2}}}{2},1)$,即$\sqrt{2}sinα-sinβ$的范围是$(-\frac{{\sqrt{2}}}{2},1)$.
点评 本题主要考查了两角和的正切函数公式,三角函数恒等变换的应用,正弦函数的图象和性质在三角函数化简求值中的应用,考查了转化思想和数形结合思想的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$ | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
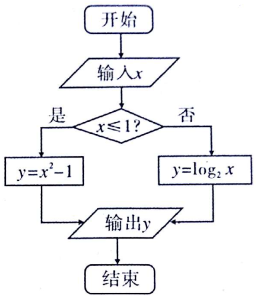 已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )| A. | [0,2] | B. | [-1,2] | C. | [-1,15] | D. | [2,15] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
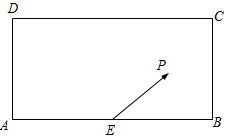 某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.
某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com