
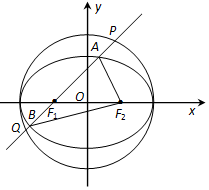
 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.分析 (1)求出c=1,设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{{{a^2}-1}}=1$,将点$({1\;,\;\frac{3}{2}})$代入,解得a2=4,然后求解椭圆C的方程.
(2)由椭圆定义,|AF1|+|AF2|=4,|BF1|+|BF2|=4,通过|AF2|,|BF2|,|AB|成等差数列,推出$|B{F_2}|=\frac{8}{3}$. 设B(x0,y0),通过$\left\{\begin{array}{l}{({x_0}-1)^2}+y_0^2=\frac{64}{9}\;,\;\\ \frac{x_0^2}{4}+\frac{y_0^2}{3}=1\;\;\end{array}\right.$解得B,然后求解直线方程,推出弦PQ的长即可.
解答 (本题满分(14分),第1小题满分(6分),第2小题满分8分)
解:(1)由题意,c=1,…(1分)
设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{{{a^2}-1}}=1$,将点$({1\;,\;\frac{3}{2}})$代入$\frac{1}{a^2}+\frac{9}{{4({a^2}-1)}}=1$,
解得a2=4(${a^2}=\frac{1}{4}$舍去),…(3分)
所以,椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$. …(4分)
(2)由椭圆定义,|AF1|+|AF2|=4,|BF1|+|BF2|=4,两式相加,得|AB|+|AF2|+|BF2|=8,
因为|AF2|,|BF2|,|AB|成等差数列,所以|AB|+|AF2|=2|BF2|,
于是3|BF2|=8,即$|B{F_2}|=\frac{8}{3}$. …(3分)
设B(x0,y0),由$\left\{\begin{array}{l}{({x_0}-1)^2}+y_0^2=\frac{64}{9}\;,\;\\ \frac{x_0^2}{4}+\frac{y_0^2}{3}=1\;\;\end{array}\right.$解得$B({-\frac{4}{3}\;,\;-\frac{{\sqrt{15}}}{3}})$,…(5分)
(或设$B(2cosθ\;,\;\sqrt{3}sinθ)$,则${(2cosθ-1)^2}+3{sin^2}θ=\frac{64}{9}$,解得$cosθ=-\frac{2}{3}$,$sinθ=-\frac{{\sqrt{5}}}{3}$,所以$B({-\frac{4}{3}\;,\;-\frac{{\sqrt{15}}}{3}})$).
所以,$k=\sqrt{15}$,直线l的方程为$y=\sqrt{15}(x+1)$,即$\sqrt{15}x-y+\sqrt{15}=0$,…(6分)
圆O的方程为x2+y2=4,圆心O到直线l的距离$d=\frac{{\sqrt{15}}}{4}$,…(7分)
此时,弦PQ的长$|PQ|=2\sqrt{4-{d^2}}=\frac{7}{2}$. …(8分)
点评 本题考查直线与椭圆的位置关系的应用,椭圆与圆的关系,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
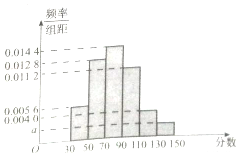 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com