
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
分析 根据平面向量的坐标运算与夹角公式,求出$\overrightarrow a+\overrightarrow b$与$\vec b$夹角的余弦值,即可求出夹角θ.
解答 解:向量$\overrightarrow a=({-1,2}),\overrightarrow b=({2,1})$,
∴$\overrightarrow a+\overrightarrow b$=(1,3),
|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=1×2+3×1=5,
又|$\vec b$|=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$,
设$\overrightarrow a+\overrightarrow b$与$\vec b$的夹角为θ,
则cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}+\overrightarrow{b}|×|\overrightarrow{b}|}$=$\frac{5}{\sqrt{10}×\sqrt{5}}$=$\frac{\sqrt{2}}{2}$,
∵$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$夹角θ的取值范围为[0,π],
∴夹角θ=45°.
故选:A.
点评 本题考查了平面向量坐标表示与夹角大小的计算问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{3}$] | B. | [$\frac{1}{3}$,1] | C. | [0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
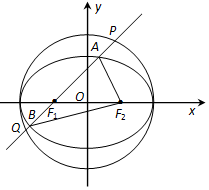 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
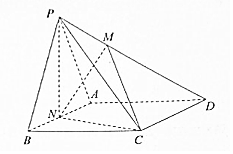 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA=PB=AB=2,点N为AB的中点.,
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA=PB=AB=2,点N为AB的中点.,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{{2\sqrt{3}}}{3}$) | B. | (1,2) | C. | (2,+∞) | D. | ($\frac{{2\sqrt{3}}}{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com