
分析 (1)直线方程与椭圆方程联立,利用判别式为0,椭圆经过当点,联立求出m,n即可得到椭圆方程.
(2)设Q(4,y0),P(x1,y1),又A(-4,0),B(4,0),求出直线AQ的方程为$y=\frac{y_0}{8}(x+4)$.联立直线与椭圆方程,利用韦达定理以及心理的数量积回家求解即可.
解答 解:(1)直线l:x+$\sqrt{2}y=4\sqrt{2}$代入椭圆C:mx2+ny2=1(n>m>0)可得:(n+2m)y2-16my+32m-1=0,
有且只有一个公共点$M[{2\sqrt{2},2}]$.△=162m2-4(n+2m)(32m-1)=0,
并且:8m+4n=1,解得m=$\frac{1}{16}$,n=$\frac{1}{8}$.
椭圆C的方程为$\frac{x^2}{16}+\frac{y^2}{8}=1$.
(2)设Q(4,y0),P(x1,y1),又A(-4,0),B(4,0),∴$\overrightarrow{OP}=({x_1},{y_1}),\overrightarrow{OQ}=(4,{y_0})$.
直线AQ的方程为$y=\frac{y_0}{8}(x+4)$.
∴$\left\{{\begin{array}{l}{\frac{x^2}{16}+\frac{y^2}{8}=1}\\{y=\frac{y_0}{8}(x+4)}\end{array}}\right.⇒(32+{y_0}^2){x^2}+8{y_0}^2•x+16{y_0}^2-32×16=0$.
∴$(-4)+{x_1}=-\frac{{8{y_0}^2}}{{32+{y_0}^2}}⇒{x_1}=4-\frac{{8{y_0}^2}}{{32+{y_0}^2}}$.
$\overrightarrow{OQ}•\overrightarrow{OP}=4{x_1}+{y_0}{y_1}$=$4{x_1}+{y_0}•\frac{y_0}{8}(x+4)$=$4({4-\frac{{8{y_0}^2}}{{32+{y_0}^2}}})+\frac{{{y_0}^2}}{8}({8-\frac{{8{y_0}^2}}{{32+{y_0}^2}}})$
=$16-\frac{{32{y_0}^2}}{{32+{y_0}^2}}+{y_0}^2-\frac{{{y_0}^4}}{{32+{y_0}^2}}=16$.
点评 本题考查向量与椭圆的关系,椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想设而不求思想方法的应用,考查计算能力.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
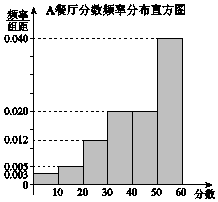 某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:| B餐厅分数频数分布表 | |
| 分数区间 | 频数 |
| [0,10) | 2 |
| [10,20) | 3 |
| [20,30) | 5 |
| [30,40) | 15 |
| [40,50) | 40 |
| [50,60] | 35 |
| 分数 | [0,30) | [30,50) | [50,60] |
| 满意度指数 | 0 | 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com