
分析 (1)求出f(x)的导数,设出切点(m,n),可得切线的斜率,由切线方程可得a,m的方程,解方程可得a=1;
(2)y=f(x)和y=x-$\frac{1}{x}$的交点为(x0,y0),分别画出y=f(x)和y=x-$\frac{1}{x}$在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.
解答 解:(1)函数f(x)=$\frac{{ax}^{2}}{{e}^{x}}$的导数为f′(x)=$\frac{a(2x{-x}^{2})}{{e}^{x}}$,
设切点为(m,n),即有n=$\frac{{am}^{2}}{{e}^{m}}$,n=$\frac{1}{e}$m,
可得ame=em,①
由直线y=$\frac{1}{e}$x为曲线y=f(x)的切线,可得$\frac{a(2m{-m}^{2})}{{e}^{m}}$=$\frac{1}{e}$,②
由①②解得m=1,a=1;
(2)函数g(x)=min{f(x),x-$\frac{1}{x}$}(x>0),
由f(x)=$\frac{{x}^{2}}{{e}^{x}}$的导数为f′(x)=$\frac{x(2-x)}{{e}^{x}}$,
当0<x<2时,f(x)递增,x>2时,f(x)递减.
对x-$\frac{1}{x}$在x>0递增,设y=f(x)和y=x-$\frac{1}{x}$的交点为(x0,y0),
由f(1)-(1-1)=$\frac{1}{e}$>0,f(2)-(2-$\frac{1}{2}$)=$\frac{4}{{e}^{2}}$-$\frac{3}{2}$<0,即有1<x0<2,
当0<x<x0时,g(x)=x-$\frac{1}{x}$,
h(x)=g(x)-cx2=x-$\frac{1}{x}$-cx2,h′(x)=1+$\frac{1}{{x}^{2}}$-2cx,
由题意可得h′(x)≥0在0<x<x0时恒成立,
即有2c≤$\frac{1}{x}$+$\frac{1}{{x}^{3}}$,由y=$\frac{1}{x}$+$\frac{1}{{x}^{3}}$在(0,x0)递减,
可得2c≤$\frac{1}{{x}_{0}}$+$\frac{1}{{{x}_{0}}^{3}}$①
当x≥x0时,g(x)=$\frac{{x}^{2}}{{e}^{x}}$,
h(x)=g(x)-cx2=$\frac{{x}^{2}}{{e}^{x}}$-cx2,h′(x)=$\frac{2x{-x}^{2}}{{e}^{x}}$-2cx,
由题意可得h′(x)≥0在x≥x0时恒成立,
即有2c≤$\frac{2-x}{{e}^{x}}$,由y=$\frac{2-x}{{e}^{x}}$,可得y′=$\frac{x-3}{{e}^{x}}$,
可得函数y在(3,+∞)递增;在(x0,3)递减,
即有x=3处取得极小值,且为最小值-$\frac{1}{{e}^{3}}$.
可得2c≤-$\frac{1}{{e}^{3}}$②,
由①②可得2c≤-$\frac{1}{{e}^{3}}$,解得c≤-$\frac{1}{{2e}^{3}}$.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查新定义的理解和运用,单调性的运用,考查分类讨论的思想方法以及恒成立问题的解法,属于综合题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-2,1) | C. | (1,+∞) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{3}$] | B. | [$\frac{1}{3}$,1] | C. | [0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
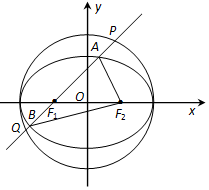 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)过点$({1\;,\;\frac{3}{2}})$,两个焦点为F1(-1,0)和F2(1,0).圆O的方程为x2+y2=a2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
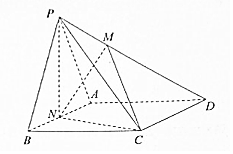 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA=PB=AB=2,点N为AB的中点.,
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA=PB=AB=2,点N为AB的中点.,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com