
分析 求出,F(0,$\frac{m}{2}$),准线方程为y=-$\frac{m}{2}$,代入双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$,可得x=±$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$,利用准线与双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$有两个交点A,B,∠AFB=120°,得出$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$=$\sqrt{3}m$,求出m,n的关系,即可得出结论.
解答 解:由题意,F(0,$\frac{m}{2}$),准线方程为y=-$\frac{m}{2}$,
代入双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$,可得x=±$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$,
∵准线与双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$有两个交点A,B,∠AFB=120°,
∴$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$=$\sqrt{3}m$,
∴m=2$\sqrt{2}$n,
∴双曲线的离心率为$\frac{\sqrt{8{n}^{2}+{n}^{2}}}{m}$=3.
故答案为3.
点评 本题考查抛物线、双曲线的方程与性质,考查学生的计算能力,确定m,n的关系是关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
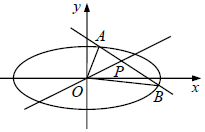 已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.
已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或-4 | B. | 2 | C. | -$\frac{1}{4}$或$\frac{1}{2}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩∁RN=φ | B. | M∪N=R | C. | ∁RM∪N=R | D. | M∩N=M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<2} | B. | {x|2<x<3} | C. | {x|x<3} | D. | {x|-1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
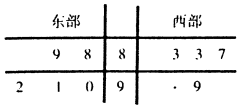 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:| 年龄x(岁) | 20 | 30 | 40 | 50 |
| 周均学习成语知识时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com