
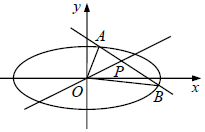
 已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.
已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.分析 (Ⅰ)由题意直线l的斜率必存在,设直线l的方程是y-$\frac{1}{2}$=k(x-t),联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系可得A,B的横坐标的和,结合点P是线段AB的中点可得k=-t,代入一元二次方程,利用判别式大于0求得t的范围,再由直线l和直线OP的倾斜角互补求得t值;
(Ⅱ)由(Ⅰ)知l的方程是$y=-tx+{t}^{2}+\frac{1}{2}$,可得S=$\frac{1}{2}({t}^{2}+\frac{1}{2})|{x}_{1}-{x}_{2}|$,化为关于t的函数求最值.
解答 解:(Ⅰ)存在.
事实上,由题意直线l的斜率必存在,设直线l的方程是y-$\frac{1}{2}$=k(x-t),
代入$\frac{{x}^{2}}{2}$+y2=1得:$(1+2{k}^{2}){x}^{2}+(2k-4{k}^{2}t)x+2(\frac{1}{2}-kt)^{2}-2=0$.①
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=-\frac{2k-4{k}^{2}t}{1+2{k}^{2}}$,
又x1+x2=2t,
∴-$\frac{2k-4{k}^{2}t}{1+2{k}^{2}}=2t$,解得:k=-t,
此时方程①为$(1+2{t}^{2}){x}^{2}-(2t+4{t}^{3})x+2(\frac{1}{2}+{t}^{2})^{2}-2=0$.
由△=$(2t+4{t}^{3})^{2}-4(1+2{t}^{2})×[2(\frac{1}{2}+{t}^{2})^{2}-2]$>0,解得0<t2<$\frac{3}{2}$,
当t=0时,显然不符合题意;
当t≠0时,设直线OP的斜率为k1,只需k1+k2=0,
即$\frac{1}{2t}+(-t)=0$,解得t=$±\frac{\sqrt{2}}{2}$,均符合题意;
(Ⅱ)由(Ⅰ)知l的方程是$y=-tx+{t}^{2}+\frac{1}{2}$,
∴S=$\frac{1}{2}({t}^{2}+\frac{1}{2})|{x}_{1}-{x}_{2}|$=$\frac{1}{2}({t}^{2}+\frac{1}{2})•\frac{\sqrt{-8{t}^{4}+8{t}^{2}+6}}{1+2{t}^{2}}$=$\frac{1}{4}\sqrt{-8{t}^{4}+8{t}^{2}+6}$,
∵0<t2<$\frac{3}{2}$,∴当${t}^{2}=\frac{1}{2}$时,${S}_{max}=\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了二次函数最值的求法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
| 广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
| 销售收入y | 16 | 23 | 25 | 26 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com