
分析 (1)设袋中原有n个白球,由题意列出方程求出n的值;
(2)由题意知ξ的可能取值为1,2,3,4,5;计算对应的概率值,列出ξ的概率分布,计算出数学期望Eξ.
解答 解:(1)设袋中原有n个白球,由题意知
$\frac{1}{7}$=$\frac{{C}_{n}^{2}}{{C}_{7}^{2}}$=$\frac{\frac{n(n-1)}{2}}{\frac{7×6}{2}}$=$\frac{n(n-1)}{7×6}$,--------3分
所以n(n-1)=6,
解得n=3或n=-2(舍去),
即袋中原有3个白球;----------6分
(2)由题意知ξ的可能取值为1,2,3,4,5.
且P(ξ=1)=$\frac{3}{7}$;
P(ξ=2)=$\frac{4×3}{7×6}$=$\frac{2}{7}$;
P(ξ=3)=$\frac{4×3×3}{7×6×5}$=$\frac{6}{35}$;
P(ξ=4)=$\frac{4×3×2×3}{7×6×5×4}$=$\frac{3}{35}$;
P(ξ=5)=$\frac{4×3×2×1×3}{7×6×5×4×3}$=$\frac{1}{35}$.
所以取球次数ξ的概率分布如下表所示:
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{7}$ | $\frac{2}{7}$ | $\frac{6}{35}$ | $\frac{3}{35}$ | $\frac{1}{35}$ |
点评 本题考查离散型随机变量的概率及概率分布与数学期望的计算问题,是综合性题目.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
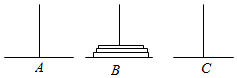 如图,汉诺塔问题是指有3根杆子A,B,C,杆上有若干碟子,把所有的碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面,把B杆上的3个碟子全部移动到A杆上,则最少需要移动的次数是( )
如图,汉诺塔问题是指有3根杆子A,B,C,杆上有若干碟子,把所有的碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面,把B杆上的3个碟子全部移动到A杆上,则最少需要移动的次数是( )| A. | 12 | B. | 9 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
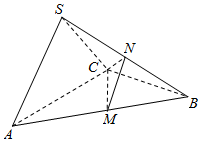 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com