
分析 利用余弦定理、基本不等式可得 3c2=a2+b2≥2ab,即 c2≥$\frac{2}{3}$ab,再利用同角三角函数的基本关系、正弦定理,把sinC•($\frac{1}{tanA}$+$\frac{1}{tanB}$)化为 $\frac{{c}^{2}}{ab}$,从而得到它的最小值.
解答 解:在△ABC中,∵已知abcosC=accosB+bccosA,∴由余弦定理可得$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2}$=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2}$+$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2}$,
即 3c2=a2+b2≥2ab,即 c2≥$\frac{2}{3}$ab,当且仅当a=b时,取等号.
则sinC•($\frac{1}{tanA}$+$\frac{1}{tanB}$)=$\frac{sinCcosA}{sinA}$+$\frac{sinCcosB}{sinB}$=$\frac{sinC(sinAcosB+cosAsinB)}{sinAsinB}$=$\frac{{sin}^{2}C}{sinAsinB}$=$\frac{{c}^{2}}{ab}$≥$\frac{2}{3}$,
即sinC•($\frac{1}{tanA}$+$\frac{1}{tanB}$)的最小值为$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题主要考查正弦定理、余弦定理、同角三角函数的基本关系,基本不等式的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$相等 | B. | 如果$\overrightarrow{a}$与$\overrightarrow{b}$平行,那么$\overrightarrow{a}$与$\overrightarrow{b}$相等 | ||
| C. | $\overrightarrow{a}$与$\overrightarrow{b}$共线 | D. | 如果$\overrightarrow{a}$与$\overrightarrow{b}$平行,那么$\overrightarrow{a}$=$\overrightarrow{b}$或$\overrightarrow{a}$=-$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 类别 | 老年教师 | 中年教师 | 青年教师 | 合计 |
| 人数 | 900 | 1800 | 1600 | 4300 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
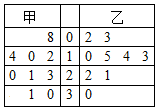 统计甲、乙两名运动员9场比赛得分情况得到茎叶图如图所示,设甲、乙得分平均数分别为$\overline{x}$,$\overline{y}$,中位数分别为m,n,则下列判断正确的是( )
统计甲、乙两名运动员9场比赛得分情况得到茎叶图如图所示,设甲、乙得分平均数分别为$\overline{x}$,$\overline{y}$,中位数分别为m,n,则下列判断正确的是( )| A. | $\overline{x}$<$\overline{y}$,m<n | B. | $\overline{x}$>$\overline{y}$,m<n | C. | $\overline{x}$>$\overline{y}$,m>n | D. | $\overline{x}$<$\overline{y}$,m>n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A?B | B. | A?B | C. | A=B | D. | A?B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com