
【题目】某公司生产某种产品的固定成本为150万元,而每件产品的可变成本为2500元,每件产品的售价为3500元,已知该公司所生产的产品能够全部销售出去.
(1)分别求出总成本![]() (万元),单位成本
(万元),单位成本![]() (万元),销售总收入
(万元),销售总收入![]() (万元),总利润
(万元),总利润![]() (万元)关于总产量x(件)的函数解析式;
(万元)关于总产量x(件)的函数解析式;
(2)由(1)所求得的函数解析式,对这个公司的经济效益作出简单分析.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 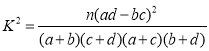 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励大家节约用水,自2013年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示.
分档 | 户年用水量 | 综合用水单价/(元· |
第一阶梯 | 0 | 3.45 |
第二阶梯 | 220 | 4.83 |
第三阶梯 | 300以上 | 5.83 |
记户年用水量为![]() 时应缴纳的水费为
时应缴纳的水费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在上海的张明一家2015年共用水![]() ,则张明一家2015年应缴纳水费多少元?
,则张明一家2015年应缴纳水费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
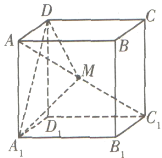
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是____.
不重合),则下列结论正确的是____.
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③![]() 的面积不可能等于
的面积不可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
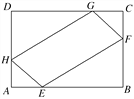
(1)写出四边形EFGH的面积y与x之间的函数关系;
(2)求当x为何值时y取得最大值,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年来,“精准扶贫”是政府的重点工作之一,某地政府对240户贫困家庭给予政府资金扶助,以发展个体经济,提高家庭的生活水平.几年后,一机构对这些贫困家庭进行回访调查,得到政府扶贫资金数、扶贫贫困家庭数![]() (户)与扶贫后脱贫家庭数
(户)与扶贫后脱贫家庭数![]() (户)的数据关系如下:
(户)的数据关系如下:
政府扶贫资金数(万元) | 3 | 5 | 7 | 9 |
政府扶贫贫困家庭数 | 20 | 40 | 80 | 100 |
扶贫后脱贫家庭数 | 10 | 30 | 70 | 90 |
(Ⅰ)求几年来该地依靠“精准扶贫”政策的脱贫率是多少;(答案精准到0.1%)
(Ⅱ)从政府扶贫资金数为3万元和7万元并且扶贫后脱贫的家庭中按分层抽样抽取8户,再从这8户中随机抽取两户家庭,求这两户家庭的政府扶贫资金总和为10万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com