
【题目】为了鼓励大家节约用水,自2013年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示.
分档 | 户年用水量 | 综合用水单价/(元· |
第一阶梯 | 0 | 3.45 |
第二阶梯 | 220 | 4.83 |
第三阶梯 | 300以上 | 5.83 |
记户年用水量为![]() 时应缴纳的水费为
时应缴纳的水费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在上海的张明一家2015年共用水![]() ,则张明一家2015年应缴纳水费多少元?
,则张明一家2015年应缴纳水费多少元?
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若直线![]() 和曲线
和曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 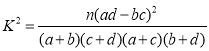 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
附:参考公式: ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为左,右焦点,
分别为左,右焦点,![]() 分别为左,右顶点,原点
分别为左,右顶点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设点
.设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() .
.
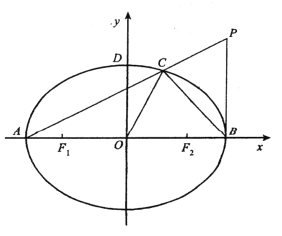
(1)求椭圆![]() 的方程;
的方程;
(2)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求直线
的面积,求直线![]() 的方程;
的方程;
(3)求过点![]() 的圆方程(结果用
的圆方程(结果用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产某种产品的固定成本为150万元,而每件产品的可变成本为2500元,每件产品的售价为3500元,已知该公司所生产的产品能够全部销售出去.
(1)分别求出总成本![]() (万元),单位成本
(万元),单位成本![]() (万元),销售总收入
(万元),销售总收入![]() (万元),总利润
(万元),总利润![]() (万元)关于总产量x(件)的函数解析式;
(万元)关于总产量x(件)的函数解析式;
(2)由(1)所求得的函数解析式,对这个公司的经济效益作出简单分析.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCD﹣A1B1C1D1为正方体,则下面结论正确的是( )
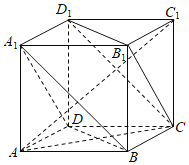
A.A1B∥B1C
B.平面CB1D1⊥平面A1B1C1D1
C.平面CB1D1∥平面A1BD
D.异面直线AD与CB1所成的角为30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com