
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积![]() (弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长
(弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长![]() 等于
等于![]() ,其弧所在圆为圆
,其弧所在圆为圆![]() ,若用上述弧田面积计算公式计算得该弧田的面积为
,若用上述弧田面积计算公式计算得该弧田的面积为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]()
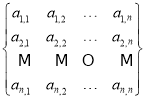 是由
是由![]() 组成的
组成的![]() 行
行![]() 列的数表(每个数恰好出现一次),
列的数表(每个数恰好出现一次),![]() 且
且![]() .
.
若存在![]() ,
, ![]() ,使得
,使得![]() 既是第
既是第![]() 行中的最大值,也是第
行中的最大值,也是第![]() 列中的最小值,则称数表
列中的最小值,则称数表![]() 为一个“
为一个“![]() 数表”
数表”![]() 为数表
为数表![]() 的一个“
的一个“![]() 值”,
值”,
对任意给定的![]() ,所有“
,所有“![]() 数表”构成的集合记作
数表”构成的集合记作![]() .
.
判断下列数表是否是“![]() 数表”.若是,写出它的一个“
数表”.若是,写出它的一个“![]() 值”;
值”;
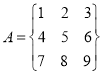 ,
, 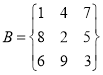
(Ⅱ)求证:若数表![]() 是“
是“![]() 数表”,则
数表”,则![]() 的“
的“![]() 值”是唯一的;
值”是唯一的;
(Ⅲ)在![]() 中随机选取一个数表
中随机选取一个数表![]() ,记
,记![]() 的“
的“![]() 值”为
值”为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题的个数是( )
①若“p∨q”为真命题,则“p∧q”为真命题;
②“a∈(0,+∞),函数y=![]() 在定义域内单调递增”的否定;
在定义域内单调递增”的否定;
③l为直线,α,β为两个不同的平面,若l⊥β,α⊥β,则l∥α;
④“x∈R,![]() ≥0”的否定为“
≥0”的否定为“![]() R,
R,![]() <0”.
<0”.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0),以椭圆短轴的一个顶点B与两个焦点F1,F2为顶点的三角形周长是4+2
(a>b>0),以椭圆短轴的一个顶点B与两个焦点F1,F2为顶点的三角形周长是4+2![]() ,且∠BF1F2=
,且∠BF1F2=![]() .
.
(1)求椭圆C的标准方程;
(2)若过点Q(1,![]() )引曲线C的弦AB恰好被点Q平分,求弦AB所在的直线方程.
)引曲线C的弦AB恰好被点Q平分,求弦AB所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为北京市居民用水阶梯水价表(单位:元/立方米).
阶梯 | 户年用水量 (立方米) | 水价 | 其中 | ||
自来水费 | 水资源费 | 污水处理费 | |||
第一阶梯 | 0-180(含) | 5.00 | 2.07 | 1.57 | 1.36 |
第二阶梯 | 181-260(含) | 7.00 | 4.07 | ||
第三阶梯 | 260以上 | 9.00 | 6.07 | ||
(Ⅰ)试写出水费![]() (元)与用水量
(元)与用水量![]() (立方米)之间的函数关系式;
(立方米)之间的函数关系式;
(Ⅱ)若某户居民年交水费1040元,求其中自来水费、水资源费及污水处理费各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com