
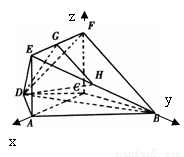
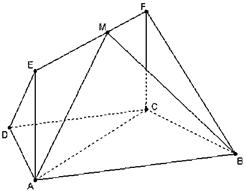
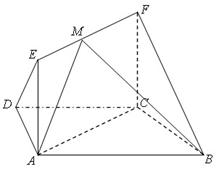
如图,在梯形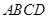 中,
中,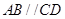 ,
,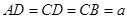 ,
,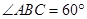 ,平面
,平面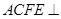 平面
平面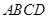 ,四边形
,四边形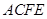 是矩形,
是矩形, ,点
,点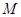 在线段EF上.
在线段EF上.
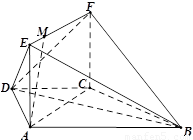
(1)求异面直线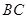 与
与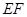 所成的角;
所成的角;
(2)求二面角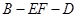 的余弦值.
的余弦值.
(1)900 ;(2)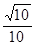 .
.
【解析】
试题分析:(1)要求异面直线所成的角,可转化为求其中一条直线与另外一直线的平行线所成的角的大小;(2)法一:利用几何法,求二面角需要先找出二面角的平面角,再在平面角所在的三角形中根据边长由余弦定理求平面角的余弦值,即二面角的余弦值;法二:利用向量法,首先建立直角坐标系,写出所需各点的坐标以及向量的坐标,再设出二面角所在两个面的法向量,利用向量垂直求出法向量的一组值,求两个法向量的夹角的余弦值,从而得二面角的余弦值.
试题解析:(1)在梯形ABCD中,∵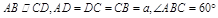 ,
,
∴四边形ABCD是等腰梯形, 且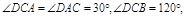
∴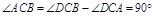 ,∴
,∴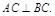
又∵平面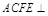 平面ABCD,交线为AC,∴
平面ABCD,交线为AC,∴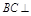 平面ACFE. ∴
平面ACFE. ∴ 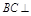 平面FE.
平面FE.
∴异面直线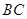 与
与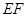 所成的角为900
7分
所成的角为900
7分
(2)方法一;(几何法)取EF中点G,EB中点H,连结DG、GH、DH,
∵容易证得DE=DF,∴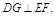
∵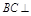 平面ACFE,∴
平面ACFE,∴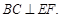 又∵
又∵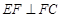 ,∴
,∴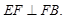
又∵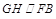 ,∴
,∴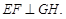
∴ 是二面角B—EF—D的平面角.
是二面角B—EF—D的平面角.
在△BDE中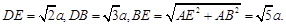
∴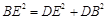 ∴
∴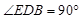 ,
,
∴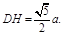 又
又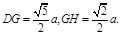 ∴在△DGH中,
∴在△DGH中,
由余弦定理得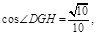 即二面角B—EF—D的平面角余弦值为
即二面角B—EF—D的平面角余弦值为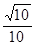 .
15分
.
15分
方法二;(向量法)以C为坐标原点,建立如图所示的直角坐标系,
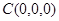 ,
,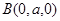 ,
,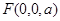 ,
,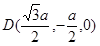 ,
,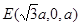
所以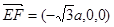 ,
,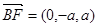 ,
,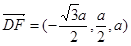
分别设平面BEF与平面DEF的法向量为
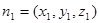 ,
,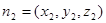
所以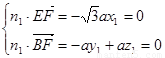 ,令
,令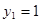 ,则
,则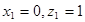
又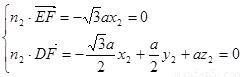 ,显然
,显然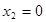 ,令
,令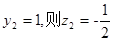
所以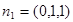 ,
,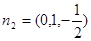 ,设二面角的平面角为
,设二面角的平面角为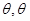 为锐角
为锐角
所以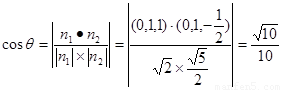 15分
15分
考点:1、异面直线所成的角;2、二面角;3、面面垂直的性质定理;4、余弦定理.


科目:高中数学 来源:2012-2013学年江苏省高三下学期期中考试数学试卷(解析版) 题型:解答题
[选修4 - 1:几何证明选讲](本小题满分10分)
如图,在梯形 中,
中,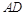 ∥BC,点
∥BC,点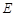 ,
, 分别在边
分别在边 ,
, 上,设
上,设 与
与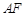 相交于点
相交于点 ,若
,若 ,
, ,
, ,
,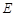 四点共圆,求证:
四点共圆,求证: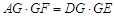 .
. 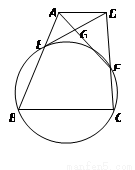
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第一次统考理科数学 题型:解答题
如图,在梯形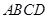 中,
中,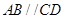 ,
,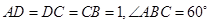 ,四边形
,四边形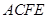 为矩
为矩
形,平面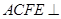 平面
平面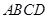 ,
,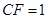 .
.
(I)求证: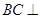 平面
平面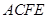 ;
;
(II)点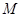 在线段
在线段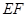 上运动,设平面
上运动,设平面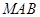 与平面
与平面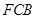 所成二面角的平面角为
所成二面角的平面角为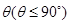 ,试求
,试求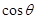
的取值范围.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第七次月考理科数学 题型:解答题
如图,在梯形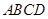 中,
中,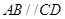 ,
,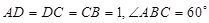 ,四边形
,四边形
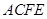 为矩形,平面
为矩形,平面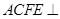 平面
平面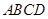 ,
,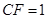 .
.
(I)求证: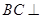 平面
平面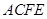 ;
;
(II)点 在线段
在线段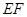 上运动,设平面
上运动,设平面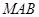 与平面
与平面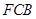 所成二面角的平面角为
所成二面角的平面角为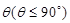 ,
,
试求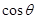 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省烟台市高三下学期3月诊断性测试理科数学 题型:解答题
(本题满分12分)
如图,在梯形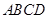 中,
中,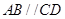 ,
,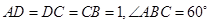 ,四边形
,四边形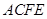 为矩形,平面
为矩形,平面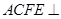 平面
平面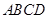 ,
,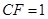 .
.
(1)求证: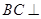 平面
平面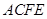 ;
;
(2)点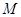 在线段
在线段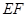 上运动,设平面
上运动,设平面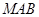 与平面
与平面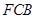 所成二面角的平面角为
所成二面角的平面角为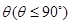 ,试求
,试求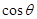 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三上学期期末考试理科数学 题型:解答题
如图,在梯形 中
中 ‖
‖ ,平面
,平面 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,点
,点 在线段
在线段 上.
上.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为何值时,
为何值时, ‖平面
‖平面 ?证明你的结论;
?证明你的结论;
(Ⅲ)求二面角 的大小.
的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com