
分析 (1)由f(x)的解析式知其图象过定点(1,0),由g(1)=0,可求得b,由f′(x)=0可求得a;
(2)要判断h(x)的符号,可分别判断f(x),g(x)的符号,g(x)=x2+x-2=(x-1)(x+2),在x>1时,g(x)>0,而对f(x)=2lnx-x+$\frac{1}{x}$,由于f(1)=0,因此由导数f′(x)判断其单调性后,再判断其正负;
(3)这里要有意识地想象此不等式的证明要利用上面的结论,考虑到当x>1时,f(x)<0,即2lnx<x-$\frac{1}{x}$,令x=$\frac{n}{n-1}$(n≥2),所以2ln$\frac{n}{n-1}$<$\frac{n}{n-1}$-$\frac{n-1}{n}$=$\frac{1}{n}$+$\frac{1}{n-1}$,让n从2开始写出n-1个不等式,相加可证,采用数学归纳法,即可证明不等式成立.
解答 解:(1)由f(x)=alnx-x+$\frac{1}{x}$,则f(x)恒过(1,0),则P(1,0),g(1)=0,
∴b=2,由f′(x)=$\frac{a}{x}$-1-$\frac{1}{{x}^{2}}$,f′(1)=0,则a=2,即a=2,b=2;
∴a,b的值2,2;
(2)h(x)=$\frac{f(x)}{g(x)}$<0,即证x>0且x≠1时,f(x),g(x)异号,
则g(x)=x2+x-2=(x-1)(x+2),
∴当x>1时,g(x)>0,则f′(x)=$\frac{2}{x}$-1-$\frac{1}{{x}^{2}}$=-$\frac{(x-1)^{2}}{{x}^{2}}$<0,
∴f(x)在(1,+∞)单调递减,
又f(1)=0,则f(x)<f(1)=0,则h(x)=$\frac{f(x)}{g(x)}$<0,
∵当0<x<1时,g(x)<0,
∴f′(x)=$\frac{2}{x}$-1-$\frac{1}{{x}^{2}}$,
∴f(x)>f(1)=0,
∴h(x)=$\frac{f(x)}{g(x)}$<0,综上得证.
(3)证明:由(2)知:当x>1时,f(x)<0,
即2lnx<x-$\frac{1}{x}$,令x=$\frac{n}{n-1}$(n≥2),
∴2ln$\frac{n}{n-1}$<$\frac{n}{n-1}$+$\frac{n-1}{n}$=$\frac{1}{n}$+$\frac{1}{n-1}$,
∴2ln$\frac{2}{1}$<$\frac{1}{2}$+1,
2ln$\frac{3}{2}$<$\frac{1}{3}$+$\frac{1}{2}$,
…
2ln$\frac{n}{n-1}$<$\frac{1}{n}$+$\frac{1}{n-1}$,
以上各式相加可得:2lnn<2(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)-1-$\frac{1}{n}$,(n>1),
1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$>lnn+$\frac{n+1}{2n}$,
另法:(3)数学归纳法证明如下:
①当n=1时,左边=1+$\frac{1}{2}$=$\frac{3}{2}$,右边=ln2+$\frac{3}{4}$,左边-右边=$\frac{3}{4}$-ln2=ln$\frac{{e}^{\frac{3}{4}}}{2}$>0,
∴左边>右边,
所以,当n=2时,不等式成立.
②假设当n=k(k≥2,k∈N*)时,不等式成立,即1+$\frac{1}{2}$+…+$\frac{1}{k}$>lnk+$\frac{k+1}{2k}$(k>1)成立.
那么,当n=k+1时,左边=1+$\frac{1}{2}$+…+$\frac{1}{k}$+$\frac{1}{k+1}$>lnk+$\frac{k+1}{2k}$+$\frac{1}{k+1}$,而右边=ln(k+1)+$\frac{k+1+1}{2(k+1)}$,
要证:1+$\frac{1}{2}$+…+$\frac{1}{k}$+$\frac{1}{k+1}$>ln(k+1)+$\frac{k+1+1}{2(k+1)}$,
即证:lnk+$\frac{k+1}{2k}$+$\frac{1}{k+1}$>ln(k+1)+$\frac{k+1+1}{2(k+1)}$,
即证:ln(k+1)-lnk<($\frac{k+1}{2k}$+$\frac{1}{k+1}$)-$\frac{k+1+1}{2(k+1)}$,即证ln$\frac{k+1}{k}$<$\frac{k+1}{2k}$-$\frac{k}{2(k+1)}$,★
由(2)知:当x>1时,h(x)<0,且g(x)>0,
∴f(x)<0,即2lnx<x-$\frac{1}{x}$,
∵$\frac{k+1}{k}$>1,
∴2l$\frac{k+1}{k}$<$\frac{k+1}{k}$-$\frac{k}{k+1}$,则★成立
∴当n=k+1时,不等式成立.
由①②知,不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$>lnn+$\frac{n+1}{2n}$(n≥2且n∈N*).
点评 本题考查导数的综合应用,考查利用导数求函数单调性,对数函数的运算性质,考查导数与不等式的综合应用,利用数学归纳法求证不等式成立.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-1,$\frac{1}{3}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-1,-$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
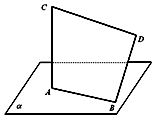 如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.
如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com