
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() .
.
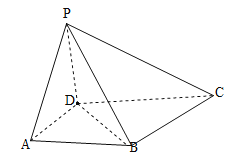
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为棱
为棱![]() 上一点,
上一点,![]() ,直线
,直线![]() 与面
与面![]() 所成角为
所成角为![]() ,试确定
,试确定![]() 的值使得
的值使得![]() .
.
科目:高中数学 来源: 题型:
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点,椭圆
是相似的两个椭圆,并且相交于上下两个顶点,椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() 长轴长是2,点
长轴长是2,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.

(1)求椭圆![]() ,
,![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在极坐标系下,已知圆O:![]() 和直线
和直线![]()
(1)求圆O和直线l的直角坐标方程;
(2)当![]() 时,求直线l与圆O公共点的一个极坐标.
时,求直线l与圆O公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭为了解冬季用电量![]() (度)与气温
(度)与气温![]() 之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出用电量![]() 关于气温
关于气温![]() 的线性回归方程;
的线性回归方程;
(2)在这5天中随机抽取两天,求至少有一天用电量低于10(度)的概率.
(附:回归直线方程的斜率和截距的最小二乘法估计公式为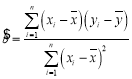 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定一个弹珠(设为质点![]() ,半径忽略不计)的运行轨迹是以小球(半径
,半径忽略不计)的运行轨迹是以小球(半径![]() )的中心
)的中心![]() 为右焦点的椭圆
为右焦点的椭圆![]() ,已知椭圆的右端点
,已知椭圆的右端点![]() 到小球表面最近的距离是1,椭圆的左端点
到小球表面最近的距离是1,椭圆的左端点![]() 到小球表面最近的距离是5.
到小球表面最近的距离是5.
 .
.
(1)求如图给定的坐标系下椭圆![]() 的标准方程;
的标准方程;
(2)弹珠由点![]() 开始绕椭圆轨道逆时针运行,第一次与轨道中心
开始绕椭圆轨道逆时针运行,第一次与轨道中心![]() 的距离是
的距离是![]() 时,弹珠由于外力作用发生变轨,变轨后的轨道是一条直线,称该直线的斜率
时,弹珠由于外力作用发生变轨,变轨后的轨道是一条直线,称该直线的斜率![]() 为“变轨系数”,求
为“变轨系数”,求![]() 的取值范围,使弹珠和小球不会发生碰撞.
的取值范围,使弹珠和小球不会发生碰撞.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线方程为
中,抛物线方程为![]() ,其顶点到焦点的距离为
,其顶点到焦点的距离为![]() .
.
(1)求抛物线的方程;
(2)若点![]() ,设直线
,设直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且直线
两点,且直线![]() 、
、![]() 的斜率之和为
的斜率之和为![]() ,试证明:对于任意非零实数
,试证明:对于任意非零实数![]() ,直线
,直线![]() 必过定点.
必过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北省第二届(荆州)园林博览会于2019年9月28日至11月28日在荆州园博园举办,本届园林博览会以“辉煌荆楚,生态园博”为主题,展示荆州生态之美,文化之韵,吸引更多优秀企业来荆投资,从而促进荆州经济快速发展.在此次博览会期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放荆州市场.已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备![]() 万台且全部售完,每万台的销售收入
万台且全部售完,每万台的销售收入![]() (万元)与年产量
(万元)与年产量![]() (万台)满足如下关系式:
(万台)满足如下关系式: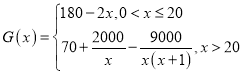 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的年利润最大?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()

(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com