
| A. | 0<k<$\frac{3}{4}$ | B. | k=$\frac{3}{4}$ | C. | k=-$\frac{3}{4}$ | D. | k>$\frac{3}{4}$ |
分析 可得点(4,-3)在渐近线y=$\frac{3}{4}$x上,数形结合可得直线与渐近线平行或无斜率时,满足题意.
解答 解:∵双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1,
∴a=4,b=3,
故其渐近线为y=$±\frac{3}{4}x$,
∵点(4,-3)在直线y=-$\frac{3}{4}$x上,
如图由双曲线的特点可知,
当直线与渐近线y=$\frac{3}{4}$x平行,满足直线与双曲线只有一个交点,
此时k═$\frac{3}{4}$,
故选:B.
点评 本题考查双曲线的性质,数形结合以及对双曲线的正确认识是解决问题的关键,属中档题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
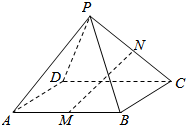 底面为平行四边形的四棱锥P-ABCD,AB=BC=14,PA=6,点M,N分别为AB,PC的中点.
底面为平行四边形的四棱锥P-ABCD,AB=BC=14,PA=6,点M,N分别为AB,PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com