
���� �����ɦ�=2sin��+4cos�ȣ��æ�2=2��sin��+4��cos�ȣ��ѻ�����ʽ���뼴�ɵó�ֱ�����귽�̣�
��������C1�ǹ����㣨1��1����һ��ֱ�ߣ����ڣ�1-2��2+��1-1��2��5���ɵõ㣨1��1��������C2���ڲ������ֱ��C1������C2һ���ཻ����ֱ�߲������̴���Բ�ķ��̿ɵã�t2-t-4=0�����ø���ϵ���Ĺ�ϵ���ҳ���ϵ���ɵó���
��� �⣺�����ɦ�=2sin��+4cos�ȣ��æ�2=2��sin��+4��cos�ȣ�
������C2��ֱ�����귽��Ϊx2+y2=2y+4x������x-2��2+��y-1��2=5��
��������C1�ǹ����㣨1��1����һ��ֱ�ߣ�
�ߣ�1-2��2+��1-1��2��5����㣨1��1��������C2�ڲ���
��ֱ��C1������C2һ���ཻ��
��$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=1+\frac{{\sqrt{3}}}{2}t\end{array}\right.$��t�Dz��������루x-2��2+��y-1��2=5����t2-t-4=0��
��t1+t2=1��t1t2=-4��
��$|AB|=|{t_1}-{t_2}|=\sqrt{{{��{t_1}+{t_2}��}^2}-4{t_1}{t_2}}=\sqrt{{1^2}+16}=\sqrt{17}$��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡�ֱ�߲������̼���Ӧ�á�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ���ҳ���ʽ��ֱ����Բ��λ�ù�ϵ��������������������������������е��⣮


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
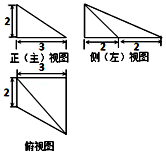
| A�� | $2\sqrt{5}$ | B�� | $4\sqrt{2}$ | C�� | $\sqrt{29}$ | D�� | $\sqrt{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
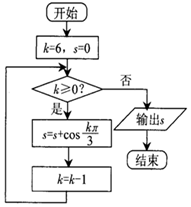
| A�� | $-\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | 0 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com