
| A. | “x2=1”是“x=1”的充分不必要条件 | |
| B. | “x=2时,x2-3x+2=0”的否命题为真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
分析 A,“x2=1”是“x=1”的必要条件;
B,“由x=1时,x2-3x+2=0可判定;
C,“<0”的否定是:“≥0”;
D,判定原命题真假,由命题的逆否命题与原命题同真假即可判定;
解答 解:对于A,“x2=1”是“x=1”的必要条件,故错;
对于B,“x=2时,x2-3x+2=0”的否命题为“x≠2时,x2-3x+2≠0”,∵x=1时,x2-3x+2=0,故错;
对于C,命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1≥0”,故错;
对于D,命题“若x=y,则sinx=siny”为真命题,故其逆否命题为真命题,故正确;
故选:D
点评 本题考查了命题真假的判定,属于基础题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
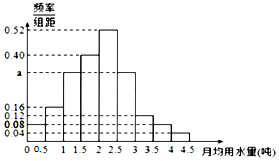 我国是世界上严重缺水的国家,某市政府为了鼓励全市30万居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费,并希望约80%的居民每月的用水量不超过标准x(吨).为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市政府为了鼓励全市30万居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费,并希望约80%的居民每月的用水量不超过标准x(吨).为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5)分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
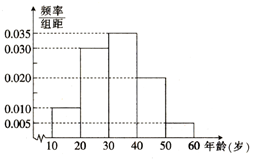 随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.
随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
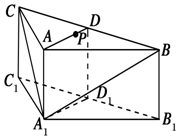 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com