
分析 (1)求出f′(x),解不等式f′(x)>0得出增区间,解不等式f′(x)<0得出减区间;
(2)求出f(x)的极值,令极大值大于0,极小值小于0解出a的范围.
解答 解:(1)f′(x)=3x2-9x+6,
令f′(x)>0得3x2-9x+6>0,解得x<1或x>2,
令f′(x)<0得3x2-9x+6<0,解得1<x<2.
∴f(x)的增区间为(-∞,1),(2,+∞),减区间为(1,2).
(2)由(1)知 当x=1时,f(x)取得极大值f(1)=$\frac{5}{2}-a$;
当x=2时,f(x)取得极小值f(2)=2-a.
∵f(x)的图象与x轴有三个交点.
∴$\left\{\begin{array}{l}{\frac{5}{2}-a>0}\\{2-a<0}\end{array}\right.$,解得:$2<a<\frac{5}{2}$.
点评 本题考查了函数单调性,极值与导数的关系,函数零点的个数判断,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
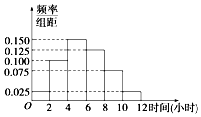 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x2=1”是“x=1”的充分不必要条件 | |
| B. | “x=2时,x2-3x+2=0”的否命题为真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | △ABC是钝角三角形 | B. | △ABC是锐角三角形 | ||
| C. | △ABC是直角三角形 | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com