
分析 由分段函数式,可得x≥0时,f(x+5k)=f(x),k为正整数,f(2017)转化为f(2)=f(-3),再代入第二段解析式,由对数的运算可得.
解答 解:由$f(x)=\left\{\begin{array}{l}f({x-5}),x≥0\\{log_3}({-x}),x<0\end{array}\right.$,
可得x≥0时,f(x+5)=f(x+5-5)=f(x),
即有f(x+5k)=f(x),k为正整数,
则f(2017)=f(403×5+2)=f(2)=f(-3)=log33=1.
故答案为:1.
点评 本题考查分段函数的函数值的求法,注意运用函数各段对应解析式,考查运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
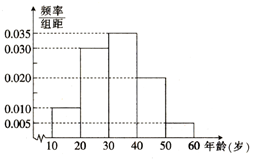 随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.
随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com