
分析 (1)利用抛物线上一点P(3,a)到焦点的距离为5,结合抛物线的定义,即可求抛物线的标准方程;
(2)设出直线l的方程为y-1=k(x+3),与抛物线方程联立化为关于x的一元二次方程,分类讨论,求出判别式等于0时k的取值,即可得出结论.
解答 解:(1)由已知设所求抛物线的方程为y2=2px(p>0),则准线方程为$x=-\frac{p}{2}$.
由定义知$\frac{p}{2}$+3=5,得p=4,
故所求方程为y2=8x. …(4分)
(2)设直线l的方程为y-1=k(x+3),
由$\left\{\begin{array}{l}y-1=k(x+3)\\{y^2}=8x\end{array}\right.$,消去x整理得ky2-8y+24k+8=0
若k=0,则解得$x=\frac{1}{8}$,y=1,
直线l与抛物线相交于一点($\frac{1}{8}$,1),直线l的方程为y=1.
若k≠0,则由题意知△=64-4k(24k+8)=0,
化简整理得3k2+k-2=0,解得k=-1或$k=\frac{2}{3}$.
此时直线l与抛物线相切于一点.
当k=-1时,直线l的方程为x+y+2=0;
当$k=\frac{2}{3}$时,直线l的方程为2x-3y+9=0.
综上所述,所求的k=0或k=-1或$k=\frac{2}{3}$,相应的直线方程分别为y=1、x+y+2=0、2x-3y+9=0. …(12分)
点评 本题考查轨迹方程,考查了直线与圆锥曲线的关系,体现了分类讨论的数学思想方法,重点是做到正确分类,是中档题.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | $[{kπ,kπ+\frac{π}{2}}]({k∈Z})$ | C. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}]({k∈Z})$ | D. | $[{kπ-\frac{π}{2},kπ}]({k∈Z})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为$\frac{\sqrt{2}}{6}$.
如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为$\frac{\sqrt{2}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
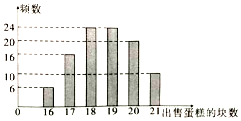 某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图:
某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com