
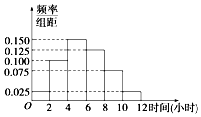
 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
分析 (1)根据分层抽样原理计算应收集的女生数;
(2)①由频率分布直方图计算对应的频率值即可;
②根据n次对立重复实验的概率模型计算概率值;
(3)计算对应的数值,填写列联表,计算观测值K2,即可得出结论.
解答 解:(1)300×$\frac{4500}{15000}$=90,所以应收集90位女生的样本数据;
(2)①由频率分布直方图得1-2×(0.100+0.025)=0.75,
所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75;
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为0.75,
从中任选三人至少有一人每周平均体育运动时间超过4小时的概率为
P=1-0.754=$\frac{175}{256}$;
(3)由(2)知,300位学生中有300×0.75=225人的每周平均体育运动时间超过4小时,
75人的每周平均体育运动时间不超过4小时,
又因为样本数据中有210份是关于男生的,90份是关于女生的,
所以每周平均体育运动时间与性别列联表如下:
每周平均体育运动时间与性别列联表
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间 不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间 超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
点评 本题主要考查频率分布直方图以及独立性检验的应用问题,是综合性题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
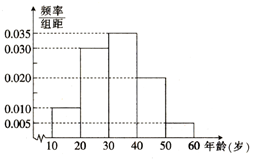 随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.
随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
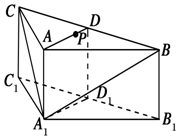 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com