
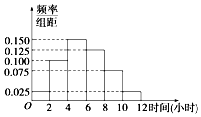
 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.分析 (Ⅰ)由频率分布直方图先求出这50个路段为中度拥堵的频率,由此能求出求出这50个路段为中度拥堵的个数.
(Ⅱ)设事件A为“一个路段严重拥堵”,则P(A)=0.1,事件B“至少一个路段严重拥堵”,P($\overline{B}$)=(1-P(A))3,由此能求出早高峰三环以内的三个路段至少有一个是严重拥堵的概率.
解答 解:(Ⅰ)由频率分布直方图得:
这50个路段为中度拥堵的有:(0.2+0.16)×1×50=18个.
(Ⅱ)设事件A为“一个路段严重拥堵”,则P(A)=0.1,
事件B“至少一个路段严重拥堵”,
则P($\overline{B}$)=(1-P(A))3=0.729,
∴早高峰三环以内的三个路段至少有一个是严重拥堵的概率:
P(B)=1-P($\overline{B}$)=1-0.729=0.271.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
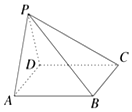 如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )
如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )| A. | $\sqrt{5}$ | B. | $4-\sqrt{5}$ | C. | $3-\sqrt{5}$ | D. | $4-2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
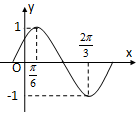 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2” | |
| B. | “x<1”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p,q均为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com