练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．在公差为d，各项均为正整数的等差数列{an}中，若a1=1，an=51，则n+d的最小值为（　　）
    A．14B．16C．18D．10

    分析 由等差数列通项公式得到d=$\frac{50}{n-1}$，由等差数列的各项均为正整数，得到d只能是1，2，5，10，25，50，n相应取得51，26，11，6，3，2，由此能求出n+d的最小值．

    解答 解：由a1=1，得到an=a1+（n-1）d=1+（n-1）d=51，
    即（n-1）d=50，
    解得：d=$\frac{50}{n-1}$，
    因为等差数列的各项均为正整数，所以公差d也为正整数，
    因此d只能是1，2，5，10，25，50，
    此时n相应取得51，26，11，6，3，2，
    则n+d的最小值等于16．
    故选：B．

    点评 本题考查等差数列的项数与公差的和的最小值的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

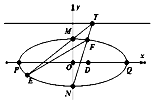    11．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的上顶点M与左、右焦点F1，F2构成三角形MF1F2面积为$\sqrt{3}$，又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$，左右顶点分别为P，Q．
    （1）求椭圆C的方程；
    （2）过点D（m，0）（m∈（-2，2），m≠0）作两条射线分别交椭圆C于A，B两点（A，B在长轴PQ同侧），直线AB交长轴于点S（n，0），且有∠ADP=∠BDQ．求证：mn为定值；
    （3）椭圆C的下顶点为N，过点T（t，2）（t≠0）的直线TM，TN分别与椭圆C交于E，F两点．若△TMN的面积是△TEF的面积的λ倍，求λ的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某重点高中拟把学校打造成新型示范高中，为此制定了学生“七不准”，“一日三省十问”等新的规章制度．新规章制度实施一段时间后，学校就新规章制度随机抽取部分学生进行问卷调查，调查卷共有10个问题，每个问题10分，调查结束后，按分数分成5组：[50，60），[50，60），[50，60），[50，60），[50，60），并作出频率分布直方图与样本分数的茎叶图（图中仅列出了得分在[50，60），[50，60）的数据）．
    （Ⅰ）求样本容量[50，60）和频率分布直方图中的[50，60）、[50，60）的值；
    （Ⅱ）在选取的样本中，从分数在70分以下的学生中随机抽取3名学生进行座谈会，求所抽取的3名学生中恰有1人得分在[50，60）内的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知抛物线E：y2=4x的焦点是F，过点F的直线l与抛物线E相交于A，B两点，O为原点．
    （Ⅰ）若直线l的斜率为1，求$\overrightarrow{OA}•\overrightarrow{OB}$的值；
    （Ⅱ）设$\overrightarrow{FB}$=t$\overrightarrow{AF}$，若t∈[2，4]，求直线l的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．命题p：若x≠0或y≠0，则x2+y2≠0，如果把命题p视为原命题，那么原命题、逆命题、否命题、逆否命题四个命题中正确命题的个数为（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

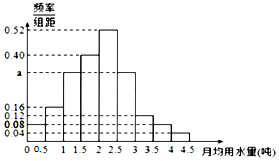    6．我国是世界上严重缺水的国家，某市政府为了鼓励全市30万居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超过x的部分按议价收费，并希望约80%的居民每月的用水量不超过标准x（吨）．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），[4，4.5）分成9组，制成了如图所示的频率分布直方图．
    （1）求直方图中a的值，并估计全市居民中月均用量不低于3吨的人数；
    （2）若每组内部，用水量视为均匀分布，估计x的值（精确到0.1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若以等边三角形ABC的顶点A，B为焦点的双曲线恰好过BC的中点，则双曲线的离心率为（　　）
    A．$\sqrt{2}$B．2C．$\sqrt{3}$D．$\sqrt{3}+1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T，其范围分为五个级别，T∈[0，2）畅通；T∈[2，4）基本畅通；  T∈[4，6）轻度拥堵；T∈[6，8）中度拥堵；T∈[8，10]严重拥堵．早高峰时段（T≥3），从某市交通指挥中心随机选取了三环以内的50个交通路段，依据其交通指数数据绘制的频率分布直方图如图．
    （Ⅰ）这50个路段为中度拥堵的有多少个？
    （Ⅱ）据此估计，早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

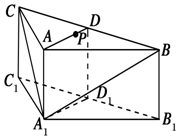    11．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB=AC，D，D1分别是线段BC，B1C1的中点，P是线段AD上异于端点的点．
    （1）在平面ABC内，试作出过点P与平面A1BC平行的直线l，并说明理由；
    （2）证明：直线l⊥平面ADD1A1．

    查看答案和解析>>

    同步练习册答案