

分析 (1)求出n的值,从而求出x,y的值即可;
(2)求出分数在[60,70)内的学生有5人,分数在[50,60)内的学生有2人,根据条件概率计算即可.
解答 解:(1)由题意可知,样本容量n=$\frac{8}{0.016×10}$=50,
y=$\frac{2}{50×10}$=0.004,
x=0.100-0.004-0.010-0.016-0.040=0.030;
(2)由题意可知,分数在[60,70)内的学生有5人,分数在[50,60)内的学生有2人,
∴所抽取的3名学生中恰有1人得分在[50,60)内的概率P=$\frac{{{C}_{2}^{1}C}_{5}^{2}}{{C}_{7}^{3}}$=$\frac{4}{7}$.
点评 本题考查了频率分布直方图,考查条件概率,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{24}{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
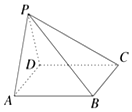 如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )
如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )| A. | $\sqrt{5}$ | B. | $4-\sqrt{5}$ | C. | $3-\sqrt{5}$ | D. | $4-2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1] | C. | (-1,0) | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2” | |
| B. | “x<1”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p,q均为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com