
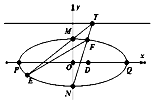
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为$\sqrt{3}$,又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$,左右顶点分别为P,Q.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为$\sqrt{3}$,又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$,左右顶点分别为P,Q.分析 (1)利用椭圆离心率三角形的面积,解得a,b,即可得到椭圆方程.
(2)设AB:y=k(x-n)(k≠0),A(x1,y1),B(x2,y2).联立直线与椭圆方程,利用韦达定理以及斜率关系,推出结果即可.
(3)设E(x3,y3),F(x4,y4),通过${S_{△TMN}}=\frac{1}{2}|{MN}||t|=|t|$,直线TM方程为:x=t(y-1),直线TN:3x-ty-t=0,联立直线与椭圆方程,求出E,F坐标,求出E到直线TN:3x-ty-t=0的距离,推出两个三角形的面积,利用基本不等式求解即可.
解答 解:(1)椭圆离心率$e=\frac{c}{a}=\frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{3}}}{2}$,又$bc=\sqrt{3},{a^2}={b^2}+{c^2}$,解得a=2,b=1,
∴椭圆$C:\frac{x^2}{4}+{y^2}=1$.
(2)由已知AB必有斜率,设AB:y=k(x-n)(k≠0),A(x1,y1),B(x2,y2).
联立$\left\{{\begin{array}{l}{y=k(x-n)}\\{{x^2}+4{y^2}=4}\end{array}}\right.⇒(4{k^2}+1)x-8{k^2}nx+4{k^2}{n^2}-4=0,{x_1}+{x_2}=\frac{{8{k^2}n}}{{4{k^2}+1}},{x_1}{x_2}=\frac{{4{k^2}{n^2}-4}}{{4{k^2}+1}}$.$∠ADP=∠BDQ⇒{k_{AD}}+{k_{BD}}=0⇒\frac{y_1}{{{x_1}-m}}+\frac{y_2}{{{x_2}-m}}=0⇒{y_1}({x_2}-m)+{y_2}({x_1}-m)=0$
⇒k(x1-n)(x2-m)+k(x1-m)(x2-m)=0⇒2x1x2-(m+n)(x1+x2)+2mn=0⇒mn=4.
(3)设E(x3,y3),F(x4,y4),因为${S_{△TMN}}=\frac{1}{2}|{MN}||t|=|t|$,
直线TM方程为:x=t(y-1),直线TN:3x-ty-t=0,
联立$\left\{{\begin{array}{l}{x=t(y-1)}\\{{x^2}+4{y^2}=4}\end{array}}\right.⇒{t^2}+4{y^2}-2{t^2}y+{t^2}-4=0⇒{y_3}•1=\frac{{{t^2}-4}}{{{t^2}+4}}⇒E(\frac{-8t}{{{t^2}+4}},\frac{{{t^2}-4}}{{{t^2}+4}})$,
联立$\left\{{\begin{array}{l}{3x=t(y+1)}\\{{x^2}+4{y^2}=4}\end{array}}\right.⇒{t^2}+36{y^2}+2{t^2}y+{t^2}-36=0⇒{y_4}•-1=\frac{{{t^2}-36}}{{{t^2}+36}}⇒F(\frac{24t}{{{t^2}+36}},\frac{{36-{t^2}}}{{36+{t^2}}})$,
所以E到直线TN:3x-ty-t=0的距离$d=\frac{{|{-\frac{24t}{{{t^2}+4}}-\frac{{t({t^2}-4)}}{{{t^2}+4}}-t}|}}{{\sqrt{{t^2}+9}}}=\frac{{2|t|{t^2}+12}}{{\sqrt{{t^2}+9}({t^2}+4)}}$,$|{TF}|=\sqrt{{{({x_4}-t)}^2}+{{({y_4}-2)}^2}}=\frac{{{t^2}+12\sqrt{{t^2}+9}}}{{{t^2}+36}}$,
∴${S_{△TEF}}=\frac{1}{2}|{TF}|d=\frac{{|t|({t^2}+6)({t^2}+12)}}{{({t^2}+18)({t^2}+2)}}$,$λ=\frac{{{S_{△TMN}}}}{{{S_{△TEF}}}}=\frac{{{t^2}+36({t^2}+4)}}{{{{({t^2}+12)}^2}}}=1+\frac{{16{t^2}}}{{{t^4}+24{t^2}+144}}=1+\frac{16}{{{t^2}+\frac{144}{t^2}+24}}≤\frac{4}{3}$
(取等条件${t^2}=12⇒t=±2\sqrt{3}$),
λ的最大值为$\frac{4}{3}$.
点评 本题考查直线与椭圆的位置关系的综合应用,椭圆的简单性质的应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 若x+y=1,则xy>1 | B. | 若x+y≠1,则xy≤1 | C. | 若x+y≠1,则xy>1 | D. | 若xy>1,则x+y≠1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{24}{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {4,6} | C. | {1,3,5} | D. | {4,6,7,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 非以上错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
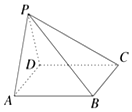 如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )
如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )| A. | $\sqrt{5}$ | B. | $4-\sqrt{5}$ | C. | $3-\sqrt{5}$ | D. | $4-2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com