
分析 根据tanα的值,利用同角三角函数间基本关系求出cotα的值,原式分子分母除以cos2α,利用同角三角函数间基本关系变形,将各自的值代入计算即可求出值.
解答 解:∵tanα=2,
∴cotα=$\frac{1}{2}$,
∴$\frac{{{{sin}^3}α-2{{cos}^3}α}}{{sinα•{{cos}^2}α}}$
=$\frac{sinα•ta{n}^{2}α-2cosα}{sinα}$
=$\frac{4sinα-2cosα}{sinα}$
=4-2×$\frac{1}{2}$
=3.
故答案是:3.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{12}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
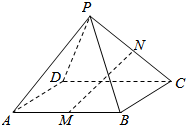 底面为平行四边形的四棱锥P-ABCD,AB=BC=14,PA=6,点M,N分别为AB,PC的中点.
底面为平行四边形的四棱锥P-ABCD,AB=BC=14,PA=6,点M,N分别为AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的部分图象如图所示,则满足f(x)≥1的x的区间为[kπ,$\frac{π}{3}$+kπ],k∈Z.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的部分图象如图所示,则满足f(x)≥1的x的区间为[kπ,$\frac{π}{3}$+kπ],k∈Z.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1.25,1.5) | B. | (1,1.25) | C. | (1.5,2) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com