求证:(1)|x-a|+|x-b|≥|a-b|,(2)|x-a|-|x-b|≤|a-b|．题目和参考答案——青夏教育精英家教网—

18．求证：
（1）|x-a|+|x-b|≥|a-b|；
（2）|x-a|-|x-b|≤|a-b|．

分析由条件利用绝对值三角不等式，证得不等式成立．

解答证明：（1）∵|x-a|+|x-b|≥|x-a-（x-b）|=|b-a|=|a-b|，
∴|x-a|+|x-b|≥|a-b|成立．
（2）∵|x-a|-|x-b|≤|（x-a）-（x-b）|=|b-a|=|a-b|，
故|x-a|-|x-b|≤|a-b|成立．

点评本题主要考查绝对值三角不等式的应用，属于基础题．

练习册系列答案

寒假新生活系列答案

寒假集训合肥工业大学出版社系列答案

寒假作业沈阳出版社系列答案

快乐天天练假期作业寒安徽师范大学出版社系列答案

走进寒假假期快乐练电子科技大学出版社系列答案

学习报快乐寒假系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

8．

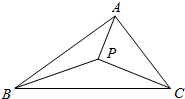如图所示，点P在已知三角形ABC的内部，定义有序实数对（μ，v，ω）为点P关于△ABC的面积坐标，其中μ=$\frac{△PBC的面积}{△ABC的面积}$，v=$\frac{△APC的面积}{△ABC的面积}$，ω=$\frac{△ABP的面积}{△ABC的面积}$；若点Q满足$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{BA}$，则点Q关于△ABC的面积坐标（$\frac{1}{2}$，$\frac{1}{6}$，$\frac{1}{3}$）．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．比较下列各组数的大小：
（1）3${\;}^{-\frac{5}{2}}$和3.1${\;}^{-\frac{5}{2}}$；
（2）-8${\;}^{-\frac{7}{8}}$和一（$\frac{1}{9}$）${\;}^{\frac{7}{8}}$；
（3）（-$\frac{2}{3}$）${\;}^{-\frac{2}{3}}$和（-$\frac{π}{6}$）${\;}^{-\frac{2}{3}}$；
（4）4.1${\;}^{\frac{2}{5}}$，3.8${\;}^{-\frac{2}{3}}$和（一1.9）${\;}^{\frac{3}{5}}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．若对于任意实数x、y总有f（xy）=f（x）+f（y），则下列各式中错误的是（　　）

A．

f（1）=0

B．

f（$\frac{1}{x}$）=f（x）

C．

f（$\frac{x}{y}$）=f（x）-f（y）

D．

f（xⁿ）=nf（x）（n∈N）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．集合A=（-∞，-1）∪（1，+∞），B={x|2x²+（2k+1）x+3k＜0}，若满足（A∩B）∩Z={2}，求实数k的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短轴长等于2$\sqrt{3}$，左焦点将长轴分为长度之比为1：3的两段．
（I）求椭圆C的方程；
（Ⅱ）若P是椭圆C上第一象限内的一点，点A，B分别为椭圆的左、右顶点，直线PA与y轴交于点M，直线PB与y轴交于点N，若△M0A与△N0B的面积之和等于6，求P点坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．某工厂生产一种电脑元件，每月的生产数据如表：