
| A. | 2($\sqrt{2}$+1) | B. | 4$\sqrt{2}$ | C. | ($\sqrt{2}$+1)2 | D. | 4($\sqrt{2}$+1)2 |
分析 由题意可得正数m、n满足$\frac{1}{m}+\frac{2}{n}$=1,整体代入可得m+n=(m+n)($\frac{1}{m}+\frac{2}{n}$)=3+$\frac{n}{m}$+$\frac{2m}{n}$,由基本不等式可得.
解答 解:∵m,n均为正数,曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1过定点A(1,$\sqrt{2}$),
∴$\frac{1}{m}+\frac{2}{n}$=1,∴m+n=(m+n)($\frac{1}{m}+\frac{2}{n}$)
=3+$\frac{n}{m}$+$\frac{2m}{n}$≥3+2$\sqrt{\frac{n}{m}•\frac{2m}{n}}$=3+2$\sqrt{2}$=($\sqrt{2}$+1)2,
当且仅当$\frac{n}{m}$=$\frac{2m}{n}$即n=$\sqrt{2}$m时取等号,
联立$\frac{1}{m}+\frac{2}{n}$=1可解得m=$\sqrt{2}$+1且n=2+$\sqrt{2}$时取等号.
故选:C.
点评 本题考查基本不等式求最值,整体代入并化为可用基本不等式的形式是解决问题关键,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
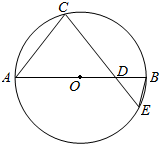 如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=2$\sqrt{2}$,BD=2.
如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=2$\sqrt{2}$,BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
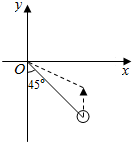 如图,据气象部门预报,在距离码头O南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动,距台风中心450km以内的地区都将受到影响.据以上预报估计,从现在起多长时间后,该码头将受到热带风暴的影响,影响时间大约有多长?(精确到0.1h,$\sqrt{2}≈$1.414)
如图,据气象部门预报,在距离码头O南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动,距台风中心450km以内的地区都将受到影响.据以上预报估计,从现在起多长时间后,该码头将受到热带风暴的影响,影响时间大约有多长?(精确到0.1h,$\sqrt{2}≈$1.414)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{x^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | C. | (3x)′=3xlog3e | D. | (x2)′=-2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com