
 在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.
在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.分析 (1)由焦点坐标及离心率可求得a、b、c即可.
(2)①利用弦长公式及韦达定理,表示出由|AB|、|CD|,由|AB|=|CD|得到m1+m2=0,
②边形ABCD 是平行四边形,设AB,CD间的距离d=$\frac{|{m}_{1}-{m}_{2}|}{\sqrt{1+{k}^{2}}}$
由m1+m2=0得s=|AB|×d=2$\sqrt{2}$$\sqrt{1+{k}^{2}}•\sqrt{\frac{2{k}^{2}-{{m}_{1}}^{2}+1}{(1+2{k}^{2})^{2}}}•$×$\frac{|2{m}_{1}|}{\sqrt{1+{k}^{2}}}$=$≤4\sqrt{2}\frac{\frac{2{k}^{2}-{{m}_{1}}^{2}+1+{{m}_{1}}^{2}}{2}}{1+2{k}^{2}}=2\sqrt{2}$.即可.
解答 解:(1)设椭圆G的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)
∵左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.∴c=1,a=$\sqrt{2}$,
b2=a2-c2=1
椭圆G 的标准方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)
①证明:由$\left\{\begin{array}{l}{y=kx+{m}_{1}}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$消去y得(1+2k2)x2+4km1x+2m12-2=0
$△=8(2{k}^{2}-{{m}_{1}}^{2}+1)>0$,
x1+x2=$\frac{-4k{m}_{1}}{1+2{k}^{2}}$,x1x2=$\frac{2{{m}_{1}}^{2}-2}{1+2{k}^{2}}$;
|AB|=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{2}$$\sqrt{1+{k}^{2}}\frac{\sqrt{2{k}^{2}-{{m}_{1}}^{2}+1}}{1+2{k}^{2}}$;
同理|CD|=2$\sqrt{2}$$\sqrt{1+{k}^{2}}\frac{\sqrt{2{k}^{2}-{{m}_{2}}^{2}+1}}{1+2{k}^{2}}$,
由|AB|=|CD|得2$\sqrt{2}$$\sqrt{1+{k}^{2}}\frac{\sqrt{2{k}^{2}-{{m}_{1}}^{2}+1}}{1+2{k}^{2}}$=2$\sqrt{2}$$\sqrt{1+{k}^{2}}\frac{\sqrt{2{k}^{2}-{{m}_{2}}^{2}+1}}{1+2{k}^{2}}$,
∵m1≠m2,∴m1+m2=0
②四边形ABCD 是平行四边形,设AB,CD间的距离d=$\frac{|{m}_{1}-{m}_{2}|}{\sqrt{1+{k}^{2}}}$
∵m1+m2=0,∴$d=\frac{|2{m}_{1}|}{\sqrt{1+{k}^{2}}}$
∴s=|AB|×d=2$\sqrt{2}$$\sqrt{1+{k}^{2}}•\sqrt{\frac{2{k}^{2}-{{m}_{1}}^{2}+1}{(1+2{k}^{2})^{2}}}•$×$\frac{|2{m}_{1}|}{\sqrt{1+{k}^{2}}}$
=$≤4\sqrt{2}\frac{\frac{2{k}^{2}-{{m}_{1}}^{2}+1+{{m}_{1}}^{2}}{2}}{1+2{k}^{2}}=2\sqrt{2}$.$4\sqrt{2}•\frac{\sqrt{(2{k}^{2}-{{m}_{1}}^{2}+1){{m}_{1}}^{2}}}{1+2{k}^{2}}$
所以当2k2+1=2m12时,四边形ABCD 的面积S 的最大值为2$\sqrt{2}$
点评 本题考查了椭圆的方程,弦长公式、韦达定理、运算能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150 | B. | 240 | C. | 360 | D. | 540 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
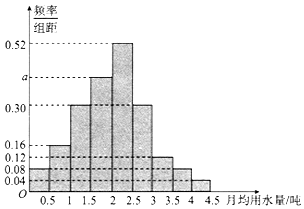 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{33}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{63}{65}$ | D. | $-\frac{33}{65}或\frac{63}{65}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com