
| A. | 150 | B. | 240 | C. | 360 | D. | 540 |
分析 根据题意,分两类,2步进行分析,将5队分为3、1、1;2、2、1的三组,再将分好的3组对应3个演习点,由排列、组合公式可得每一步的情况数目,由分步计数原理,计算可得答案.
解答 解:根据题意,个消防队分配到这3个演习点,若每个演习点至少安排1个消防队,则
可将5队分为3、1、1的三组,有$\frac{{C}_{5}^{3}{C}_{2}^{1}}{{A}_{2}^{2}}$=10种分组方法,将分好的3组对应对应3个演习点,有A33=6种方法,
共有10×6=60种分配方案;
将5队分为2、2、1的三组,有$\frac{{C}_{5}^{2}{C}_{3}^{2}}{{A}_{2}^{2}}$=15种分组方法,将分好的3组对应对应3个演习点,有A33=6种方法,
共有15×6=90种分配方案;
故共有60+90=150种分配方案.
故选:A.
点评 本题考查排列、组合的运用,关键是根据“每个演习点至少安排1个消防队”的要求,明确要将将5个队分为3、1、1;2、2、1的三组.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q为真 | B. | p∨q为真 | C. | p∧(¬q)为假 | D. | (¬p)∧(¬q)为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
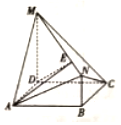 如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.
如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.
在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6米/秒 | B. | 7米/秒 | C. | 8米/秒 | D. | 9米/秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}-4}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com