
【题目】给出下列命题:
(1)函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
(2)函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
(3)函数![]() 是偶函数;
是偶函数;
(4)存在实数![]() ,使
,使![]() ;
;
(5)如果函数![]() 的图象关于点
的图象关于点![]() 中心对称,那么
中心对称,那么![]() 的最小值为
的最小值为![]() .
.
其中正确的命题的序号是___________.
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在个矩形ABCD的池底水平铺设污水净化管道(![]() ,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且
,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且![]() ,
,![]() ,设
,设![]() .
.
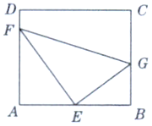
(1)试将污水管道的长度l表示成![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 为何值时,污水净化效果最好,并求此时管道的长度.
为何值时,污水净化效果最好,并求此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.
(1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果![]() ,且
,且![]() ,
,![]() ,那么
,那么![]() ;
;
(2)请你运用上述对数运算性质计算![]() 的值;
的值;
(3)因为![]() ,所以
,所以![]() 的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断
的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断![]() 的位数.(注
的位数.(注![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业2017年招聘员工,其中![]() 五种岗位的应聘人数、录用人数和录用比例(精确到
五种岗位的应聘人数、录用人数和录用比例(精确到![]() )如下:
)如下:
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
总计 | 533 | 264 |
| 467 | 169 |
|
(Ⅰ)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;
(Ⅱ)从应聘![]() 岗位的6人中随机选择2人.记
岗位的6人中随机选择2人.记![]() 为这2人中被录用的人数,求
为这2人中被录用的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)表中![]() 各岗位的男性、女性录用比例都接近(二者之差的绝对值不大
各岗位的男性、女性录用比例都接近(二者之差的绝对值不大![]() ),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法的错误的是( )
A. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
B. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
C. 不经过原点的直线的方程都可以表示为![]()
D. 经过任意两个不同的点![]() 、
、![]() 直线的方程都可以表示为
直线的方程都可以表示为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:方程x2+(2m-4)x+m=0有两个不等的实数根:命题q:x∈[2,3],不等式x2-4x+13≥m2恒成立.
(1)若命题p为真命题,则实数m的取值范围;
(2)若命题p∨q为真命题,命题p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com