
分析 x2-y2-2x=0可化为(x-1)2-y2=1;x′2-16y′2-4x′=0可化为( $\frac{1}{2}$x′-1)2-(2y′)2=1;从而得到.
解答 解:∵x2+y2-2y=0可化为(y-1)2+x2=1;
16x′2+y′2-4y′=0可化为($\frac{1}{2}$y′-1)2+(2x′)2=1;
∴$\left\{\begin{array}{l}{x=2x′}\\{y=\frac{1}{2}y′}\end{array}\right.$,解得$\left\{\begin{array}{l}{x′=\frac{1}{2}x}\\{y′=2y}\end{array}\right.$,
即:曲线x2+y2-2y=0$\stackrel{横坐标缩短为原来的2倍,纵坐标伸长为原来的2倍}{→}$16x′2+y′2-4y′=0.
故答案为:横坐标缩短为原来的2倍,纵坐标伸长为原来的2倍.
点评 本题考查了图象的伸缩变换的应用,属于基础题.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | (-8,6) | B. | (8,-6) | C. | (-8,-6)或(8,6) | D. | (-8,6)或(8,-6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 10 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,3) | B. | {-3,3} | C. | {x|x≠±3} | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=8sin(3x+$\frac{π}{4}$) | B. | y=5sin($\frac{7}{4}$π-2x) | C. | y=5sin2(x+$\frac{π}{4}$) | D. | y=5sin3(x-$\frac{7π}{12}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
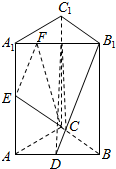 如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.
如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\sqrt{3},0)$,$(-\sqrt{3},0)$ | B. | (1,0),(-1,0) | C. | $(-\frac{{\sqrt{6}}}{2},0)$,$(\frac{{\sqrt{6}}}{2},0)$ | D. | $(-\frac{{\sqrt{2}}}{2},0)$,$(\frac{{\sqrt{2}}}{2},0)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com