
【题目】定义在![]() 上的函数
上的函数![]() 满足对任意
满足对任意![]() ,
,![]() 成立,当
成立,当![]() 时,
时,![]() ,则在
,则在![]() 内,函数
内,函数![]() 的所有零点之和为________
的所有零点之和为________
【答案】![]()
【解析】
根据题中的条件得到函数的解析式为:f(x)=﹣x+2b,x∈(b,2b],分类讨论在[1,2018]内,函数![]() 的各个零点的值,可得答案.
的各个零点的值,可得答案.
解:因为对任意的x∈(0,+∞)恒有f(2x)=2f(x)成立,
且当x∈(1,2]时,f(x)=2﹣x,
所以f(x)=﹣x+2b,x∈(b,2b].
当x∈(![]() ,1]时,由函数
,1]时,由函数![]() 1=0得:x
1=0得:x![]() [1,2018];
[1,2018];
当x∈(1,2]时,由函数![]() 2=0得:x
2=0得:x![]() ∈[1,2018];
∈[1,2018];
当x∈(2,4]时,由函数![]() 4=0得:x=3∈[1,2018];
4=0得:x=3∈[1,2018];
当x∈(4,8]时,由函数![]() 8=0得:x=6∈[1,2018];
8=0得:x=6∈[1,2018];
当x∈(8,16]时,由函数![]() 16=0得:x=12∈[1,2018];
16=0得:x=12∈[1,2018];
当x∈(16,32]时,由函数![]() 32=0得:x=24∈[1,2018];
32=0得:x=24∈[1,2018];
当x∈(32,64]时,由函数![]() 64=0得:x=48∈[1,2018];
64=0得:x=48∈[1,2018];
当x∈(64,128]时,由函数![]() 128=0得:x=96∈[1,2018];
128=0得:x=96∈[1,2018];
当x∈(128,256]时,由函数![]() 256=0得:x=192∈[1,2018];
256=0得:x=192∈[1,2018];
当x∈(256,512]时,由函数![]() 512=0得:x=384∈[1,2018];
512=0得:x=384∈[1,2018];
当x∈(512,1024]时,由函数![]() 1024=0得:x=768∈[1,2018];
1024=0得:x=768∈[1,2018];
当x∈(1024,2048]时,由函数![]() 2048=0得:x=1536∈[1,2018];
2048=0得:x=1536∈[1,2018];
故函数![]() 的所有零点之和为
的所有零点之和为![]() 3+6+12+24+48+96+192+384+768+1536=3070.5
3+6+12+24+48+96+192+384+768+1536=3070.5
故答案为:3070.5


科目:高中数学 来源: 题型:
【题目】已知曲线![]() (
(![]() 为常数).
为常数).
(i)给出下列结论:
①曲线![]() 为中心对称图形;
为中心对称图形;
②曲线![]() 为轴对称图形;
为轴对称图形;
③当![]() 时,若点
时,若点![]() 在曲线
在曲线![]() 上,则
上,则![]() 或
或![]() .
.
其中,所有正确结论的序号是_________.
(ii)当![]() 时,若曲线
时,若曲线![]() 所围成的区域的面积小于
所围成的区域的面积小于![]() ,则
,则![]() 的值可以是_________.(写出一个即可)
的值可以是_________.(写出一个即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环境保护部门对某处的环境状况用“污染指数”来监测,据测定,该处的“污染指数”与附近污染源的强度和距离之比成正比,比例系数为常数![]()
![]() ,现已知相距
,现已知相距![]() 的
的![]() 两家化工厂(污染源)的污染强度分别为1和
两家化工厂(污染源)的污染强度分别为1和![]()
![]() ,它们连线段上任意一点
,它们连线段上任意一点![]() 处的污染指数
处的污染指数![]() 等于两化工厂对该处的污染指数之和,设
等于两化工厂对该处的污染指数之和,设![]() ;
;
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() 时,
时,![]() 处的“污染指数”最小,试求
处的“污染指数”最小,试求![]() 化工厂的污染强度
化工厂的污染强度![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,我们知道当a取不同的值时,得到不同的数列.如当
,我们知道当a取不同的值时,得到不同的数列.如当![]() 时,得到无穷数列:0,
时,得到无穷数列:0,![]() ,
,![]() ,
,![]() ,…,当
,…,当![]() 时,得到有穷数列:
时,得到有穷数列:![]() ,
,![]() ,1.
,1.
(1)当a为何值时,![]() ;
;
(2)设数列![]() 满足
满足![]() ,
,![]() ,求证:a取
,求证:a取![]() 中的任一数,都可以得到一个有穷数列
中的任一数,都可以得到一个有穷数列![]() ;
;
(3)是否存在实数a,使得到的![]() 是无穷数列,且对于任意
是无穷数列,且对于任意![]() ,都有
,都有![]() 成立,若存在,求出a的取值范围;若不存在,请说明理由.
成立,若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每个国家身高正常的标准是不一样的,不同年龄、不同种族、不同地区身高都是有差异的,我们国家会定期进行0~18岁孩子身高体重全国性调查,然后根据这个调查结果制定出相应的各个年龄段的身高标准.一般测量出一个孩子的身高,对照一下身高体重表,如果在平均值标准差以内的就说明你的孩子身高是正常的,否则说明你的孩子可能身高偏矮或偏高了.根据科学研究0~18岁的孩子的身高服从正态分布![]() .在某城市随机抽取100名18岁男大学生得到其身高(
.在某城市随机抽取100名18岁男大学生得到其身高(![]() )的数据.
)的数据.
(1)记![]() 表示随机抽取的100名18岁男大学生身高的数据在
表示随机抽取的100名18岁男大学生身高的数据在![]() 之内的人数,求
之内的人数,求![]() 及
及![]() 的数学期望.
的数学期望.
(2)若18岁男大学生身高的数据在![]() 之内,则说明孩子的身高是正常的.
之内,则说明孩子的身高是正常的.
(i)请用统计学的知识分析该市18岁男大学生身高的情况;
(ii)下面是抽取的100名18岁男大学生中20名大学生身高(![]() )的数据:
)的数据:
1.65 | 1.62 | 1.74 | 1.82 | 1.68 | 1.72 | 1.75 | 1.66 | 1.73 | 1.67 |
1.86 | 1.81 | 1.74 | 1.69 | 1.76 | 1.77 | 1.69 | 1.78 | 1.63 | 1.68 |
经计算得![]() ,
, ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个学生的身高,
个学生的身高,![]() .用样本平均数
.用样本平均数![]() 作为
作为![]() 的估计值,用样本标准差
的估计值,用样本标准差![]() 作为
作为![]() 的估计,剔除
的估计,剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() 的值.(精确到0.01)
的值.(精确到0.01)
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆黄金周影市火爆依旧,《我和我的祖国》、《中国机长》、《攀登者》票房不断刷新,为了解我校高三2300名学生的观影情况,随机调查了100名在校学生,其中看过《我和我的祖国》或《中国机长》的学生共有80位,看过《中国机长》的学生共有60位,看过《中国机长》且看过《我和我的祖国》的学生共有50位,则该校高三年级看过《我和我的祖国》的学生人数的估计值为( )
A.1150B.1380C.1610D.1860
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由![]() 个不同的数构成的数列
个不同的数构成的数列![]() 中,若
中,若![]() 时,
时,![]() (即后面的项
(即后面的项![]() 小于前面项
小于前面项![]() ),则称
),则称![]() 与
与![]() 构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为
构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为![]() ;同理,等比数列
;同理,等比数列![]() 的逆序数为
的逆序数为![]() .
.
(1)计算数列![]() 的逆序数;
的逆序数;
(2)计算数列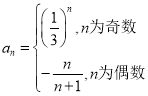 (
(![]() )的逆序数;
)的逆序数;
(3) 已知数列![]() 的逆序数为
的逆序数为![]() ,求
,求![]() 的逆序数.
的逆序数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:![]() 与直线
与直线![]() 交于A、B两点.
交于A、B两点.
(1)当![]() 取得最小值为
取得最小值为![]() 时,求
时,求![]() 的值.
的值.
(2)在(1)的条件下,过点![]() 作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且
作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且![]() 的平分线与
的平分线与![]() 轴平行,求证:直线MN的斜率为定值.
轴平行,求证:直线MN的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com