
| A. | ${a_n}=\frac{1}{n}$ | B. | ${a_n}=\frac{1}{n+1}$ | C. | an=n | D. | ${a_{n+1}}=\frac{1}{n}$ |
分析 利用递推关系式可求出a2,a3,a4,…,进而猜想归纳出其通项公式
解答 解:由题意可得:a1=1,且an+1=$\frac{a_n}{{1+{a_n}}}$,
则a2=$\frac{1}{1+1}$=$\frac{1}{2}$,a3=$\frac{\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$,a4=$\frac{\frac{1}{3}}{1+\frac{1}{3}}$=$\frac{1}{4}$
…
∴通过观察归纳出规律:其通项应是一个真分数,分子为1,分母与相应的下标相同,
故an=$\frac{1}{n}$(n∈N*).
可用数学归纳法或取倒数法加以证明,
故选:A
点评 正确理解递推关系并求出数列的前几项和使用归纳推理是解题的关键


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 3 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\sqrt{2}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\sqrt{5}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )| A. |  | B. |  | C. | 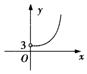 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com