
设函数f(x)=2x3-3(a-1)x2+1,其中a≥1.求函数f(x)的单调区间和极值.
详见解析.
【解析】
试题分析:(1)先求导数fˊ(x),求出f′(x)=0的值,然后讨论a=1与a>1两种情形,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,从而的函数f(x)的单调区间;(2)讨论a=1与a>1两种情形,根据(1)可知f′(x)=0的点附近的导数的符号的变化情况,从而的函数f(x)的极值.
由已知得f?(x)=6x[x-(a-1)],令f?(x)=0,解得 x1=0,x2=a-1,.
(1)当a=1时,f?(x)=6x2,f(x)在(-∞,+∞)上单调递增
当a>1时,f?(x)=6x[x-(a-1)],f?(x),f(x)随x的变化情况如下表:
x | (-∞,0) | 0 | (0,a-1) | a-1 | (a-1,+∞) |
f?(x) | + | 0 |
| 0 |
|
f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
从上表可知,函数f(x)在(-∞,0)上单调递增;在(0,a-1)上单调递减;在(a-1,+∞)上单调递增.
(2)由(1)知,当a=1时,函数f(x)没有极值.;当a>1时,函数f(x)在x=0处取得极大值,在x=a-1处取得极小值1-(a-1)3.
考点:利用导数研究函数的单调性.


科目:高中数学 来源:2015届山东广饶一中高二上学期期末质量检测文科数学试卷B(解析版) 题型:选择题
设变量 、
、 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值是( )
的最小值是( )
A.-7 B.-4 C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2015届安徽师大附中高二下学期期中考查理科数学试卷(解析版) 题型:选择题
已知 =(2,4,5),
=(2,4,5), =(3,x,y),若
=(3,x,y),若 ∥
∥ ,则( )
,则( )
A.x=6,y=15
B.x=3,y=
C.x=3,y=15
D.x=6,y=
查看答案和解析>>
科目:高中数学 来源:2015届安徽师大附中高二下学期期中考查文科数学试卷(解析版) 题型:选择题
若抛物线
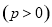 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A.8 B.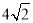 C.4 D.2
C.4 D.2
查看答案和解析>>
科目:高中数学 来源:2015届宁夏高二下学期期中考试理科数学试卷(解析版) 题型:选择题
一物体在力 (单位:N)的作用下沿与力
(单位:N)的作用下沿与力 相同的方向,从x=0处运动到
相同的方向,从x=0处运动到 (单位:
(单位:  )处,则力
)处,则力 做的功为( )
做的功为( )
A.44 B.46 C.48 D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com