Question

11．△ABC中，∠BAC=45°，AD⊥BC于D，BD=2，DC=3，则AC边上中线BE的长等于$\frac{\sqrt{85}}{2}$．

Answer 1

分析 设∠BAD=θ，则∠DAC=$\frac{π}{4}$-θ，在Rt△ABD中，可得AD=$\frac{2}{tanθ}$，在Rt△ACD中，可得AD=$\frac{3}{tan（\frac{π}{4}-θ）}$，从而$\frac{2}{tanθ}$=$\frac{3}{tan（\frac{π}{4}-θ）}$，解得tan$θ=\frac{1}{3}$，进而解得AD，由勾股定理可求AE，AB，利用余弦定理即可解得BE的值．

解答 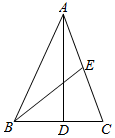解：设∠BAD=θ，则∠DAC=$\frac{π}{4}$-θ，
∵AD⊥BC，
∴在Rt△ABD中，tanθ=$\frac{BD}{AD}$，即AD=$\frac{2}{tanθ}$；
在Rt△ACD中，tan（$\frac{π}{4}$-θ）=$\frac{CD}{AD}$，即AD=$\frac{3}{tan（\frac{π}{4}-θ）}$，
∴$\frac{2}{tanθ}$=$\frac{3}{tan（\frac{π}{4}-θ）}$，解得tan$θ=\frac{1}{3}$，可得：AD=6．
∴AE=$\frac{1}{2}AC$=$\frac{1}{2}$$\sqrt{{6}^{2}+{3}^{2}}$=$\frac{3}{2}$$\sqrt{5}$，AB=$\sqrt{B{D}^{2}+A{D}^{2}}=\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$．
∴在△ABE中，由余弦定理可得：BE²=AB²+AE²-2AB$•AE•cos\frac{π}{4}$=$\frac{85}{4}$，
∴解得BE=$\frac{\sqrt{85}}{2}$．
故答案为：$\frac{\sqrt{85}}{2}$．

点评 本题主要考查了三角函数的定义，勾股定理，余弦定理在解三角形中的综合应用，考查了转化思想和数形结合思想，属于中档题．