
| A. | $\sqrt{6}$ | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}$+2 | D. | 3 |
分析 由已知,PA,PB,PC两两垂直,点P在直径为$\sqrt{2}$的球面上,球直径等于以PA,PB,PC为棱的长方体的对角线,得到2PB2+PC2=2,再结合三角换元法,由三角函数的性质得到PA+PB+PC的最大值.
解答 解:∵PA,PB,PC两两垂直,点P在直径为$\sqrt{2}$的球面上,
∴以PA,PB,PC为棱的长方体的对角线即为球的一条直径.
∴2=PA2+PB2+PC2,又PA=PB,∴2PB2+PC2=2,
设PB=cosα,PC=$\sqrt{2}$sinα,
则PA+PB+PC=2PB+PC=2cosα+$\sqrt{2}$sinα=$\sqrt{6}$sin(α+φ)≤$\sqrt{6}$.
则PA+PB+PC的最大值为$\sqrt{6}$,
故选:A.
点评 本题考查球的内接几何体,其中根据已知条件,得到棱锥的外接球直径等于以PA,PB,PC为棱的长方体的对角线,是解答本题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [$\frac{π}{2}$,$\frac{5π}{6}$] | D. | [$\frac{2π}{3}$,π] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 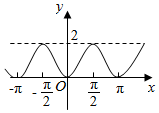 | B. | 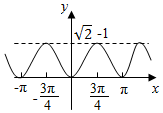 | ||
| C. | 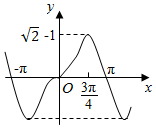 | D. | 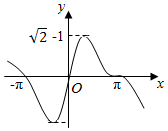 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com